Only your data knows for sure as there may be a weekly deterministic effect (seasonal pulses) and other "features" waiting to be discovered .... post your data and I will try and help further .. The acf and pacf are descriptive but only inferential iff ...no pulses , no level/step shifts , no seasonal pulses . no local time trends , constant error variance and parameters over time
after receipt of your data ( 366 days  ily values for 1 year ) .
In summary ...when you have daily data there could be
ily values for 1 year ) .
In summary ...when you have daily data there could be
- day-of-the-week effects not provable with your data
- week-of-the-year effects not provable with your data
- month-of-the-year effects provable
- day-of-the-month effects not provable with your data
- week-if-the-month effects not provable with your data
- holiday effects not provable with your data
- long weekend effects not provable with your data
- level shift effects not significant
- local time trends not significant
- arima effects not significant
- differencing effects not significant
- pulse effects significant
- paramater changes over time not provable with your data
- power transform effects significant
15 deterministic error var change not provable with your data
16 exogenous variables effect not provable with your data
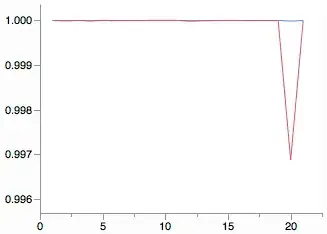
The software I used identified a number of pulses ...1 period anomalies . See the Actual and Cleansed graph here  . The cleansed series led directly to a seasonal model with 10 predictors using a log transformation
. The cleansed series led directly to a seasonal model with 10 predictors using a log transformation 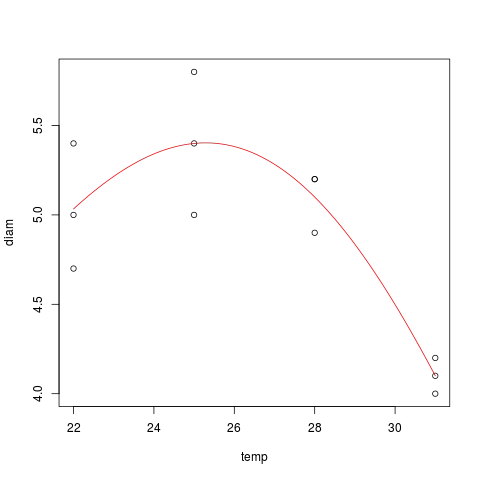 .
.
The plot of the residuals is here 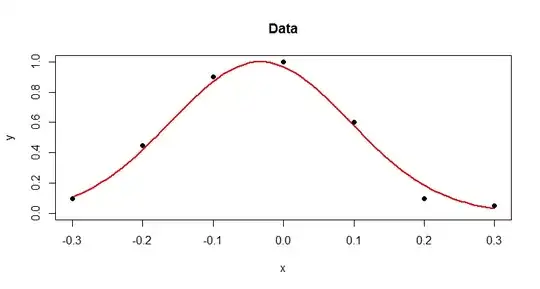 suggesting reduced variablity during the summer months. The residual acf is here
suggesting reduced variablity during the summer months. The residual acf is here 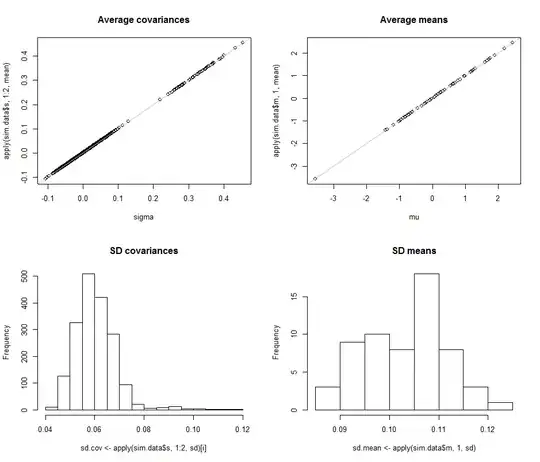
Responding directly to your question the best arima model is (0,0,0)(0,0,0) with 10 Monthly Seasonal Indicators reflecting deterministic changes through the year.
The pulses that were identified are here : 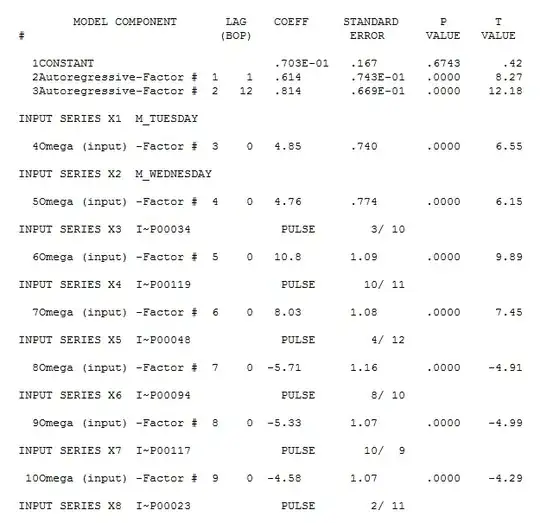 and model summary here
and model summary here