ARIMA with independent variables

Question

I'm a Data Scientist, but new to time series methods. I primarily use SPSS, but I'm familiar with R.

I have read Rob's blog, various books, and taken a few courses. I have a couple of outstanding questions for which I'm seeking assistance:

1. I have independent variables that I would like to use as predictors - I have used first differencing to make them "stationary"; it seems to have worked. Is this an appropriate step. Also, it seems that SPSS (or auto.arima in R) will do this step for you. (also: SPSS doesn't have the adf.test function for stationarity, so I have to export my data to R to do that)

2. All of my predictors had an ACF/PCF which suggested a first-order AR term. The dependent variable was an AR(3) process. However, when I used the auto.arima function (or SPSS expert modeler), none of the independent variables were significant. However, if I manually specified the transfer function in SPSS, then several of the lagged predictors did become significant. How is that possible?

3. I'm not sure if I'm missing something in this process. It seems that if my Y is stationary, and my x's (independents) are stationary, then the modeling should pick up significant predictors (if there are any).

I can post raw data / SPSS output if that would help.

Thanks for anyone who takes the time to respond!

EDIT - adding graphs and data

This is the ACF Plot of the dependent variable

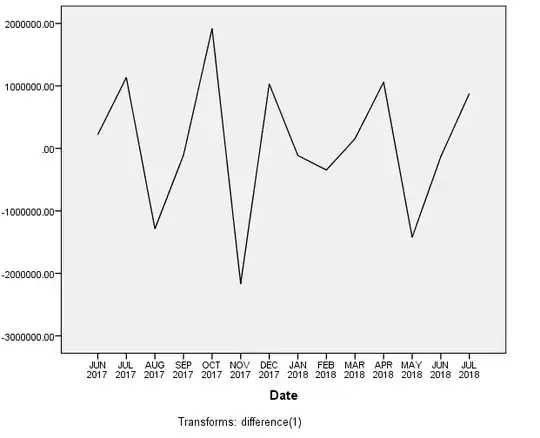
This is the DV sequence plot after first-order differencing to remove trend

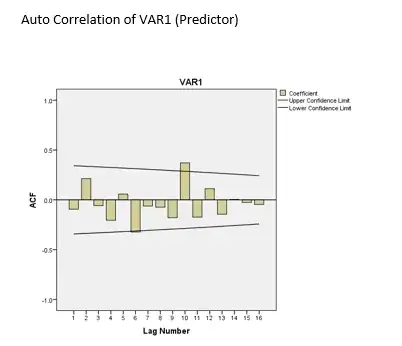
This is the ACF plot of the IV (predictor) showing a likely AR(1) process

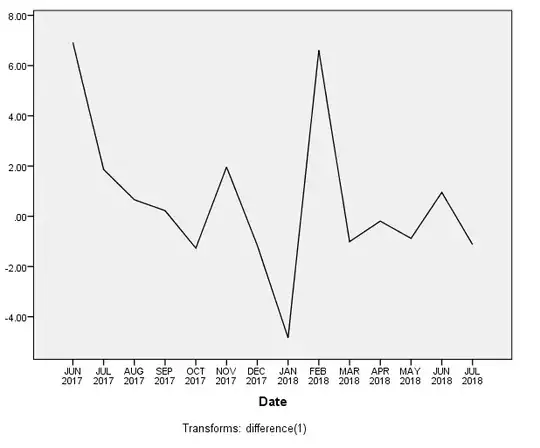
This is the sequence plot after first-order differencing to remove trend

SPSS Output using the ARIMA "Expert Modeler". The model found an AR(3) process for the DV (revenue) but none of the other 3 predictor variables were found to be statistically significant*

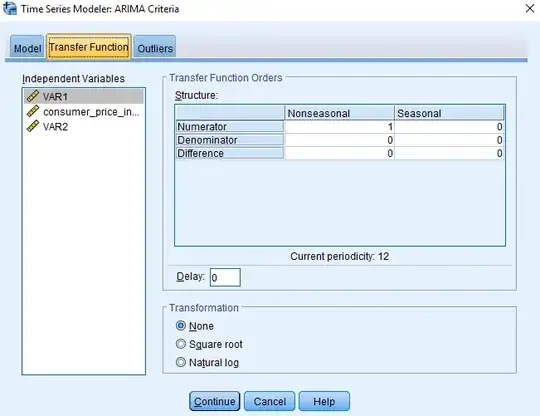
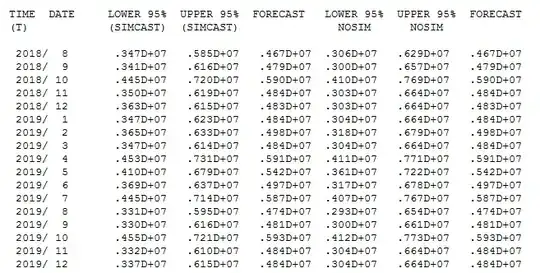
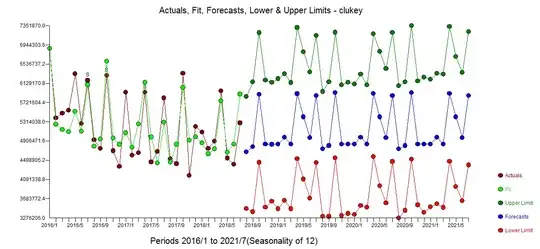
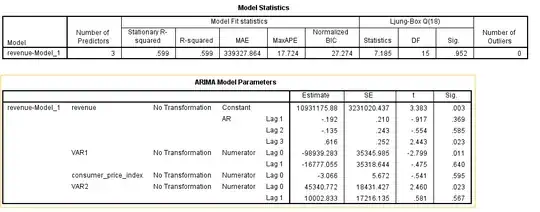
SPSS Output using a custom Transfer Model. If, instead, I customize the ARIMA model I get significant results. The same covariates were used as in the model above. The only difference is that I specified the numerator of the transfer function as "1", to be consistent with the ACF plots and their respective AR process

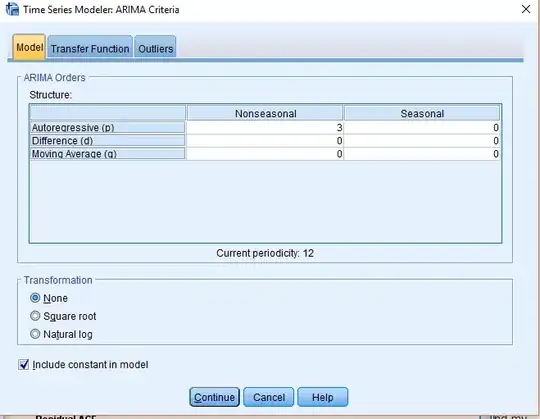
Below are the windows where I specified the transfer function. There are two - one where you specify the transfer function of the model (for the DV) and a second window where you can specify the transfer function parameters for each individual IV

so my question is... what am I doing wrong. Or have I misundertood something about modeling indpendent variables in an ARIMA process?

I'm not sure if I can upload the raw data, but I'm happy to share it if anyone would like to run the numbers themselves.

Answer 1

post your data in a csv format . If you can't then email it to me and I will take a look . In general the nature of X or Y ( in terms of stationarity ) has nothing whatsoever to do with the functional form relating X to Y . However when one identifies the form of the relationship one needs to transform X and Y appropriately This is discussed here Why is prewhitening important?… . Another discussion Transfer function in forecasting models - interpretation might also help.

EDITED AFTER RECEIPT OF DATA:

I took your 31 monthly values for the 4 series and introduced them to AUTOBOX , a piece of time series software that I have helped to develop. It developed pre-whitening models for all 4 series and developed the following model .

Not terribly different from your SPSS model but it did detect 3 seasonal pulses which are very important in making a useful forecast.

The residual from the model are here and a table of forecasts is presented here including the uncertainty in the three predictor series.

The Actual/Fit and Forecast is here ....