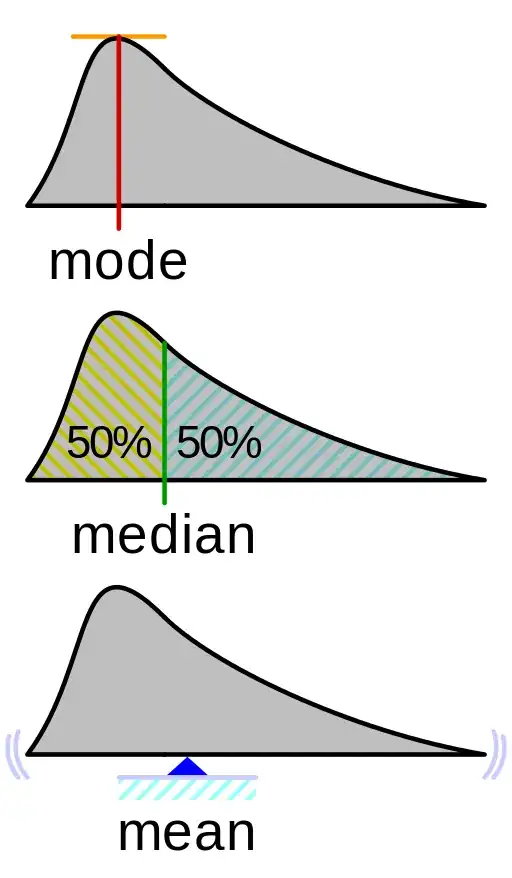
Is there any nice geometric interpretation of the mathematical expectation of a random variable (preferably based on density or cumulative density plot)?
(For example, median has a nice geometric interpretation as the point dividing the area under the density curve into two parts of equal size. Meanwhile, mode corresponds to the highest point of the density. But what about the mathematical expectation?)