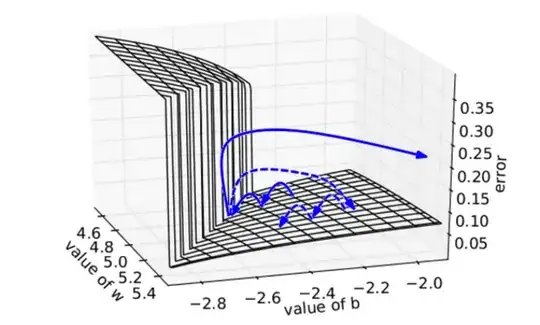
In the book "Deep Learning" by Goodfellow, Bengio, and Courville, I do not understand the following statement about why nonlinearities in deep neural nets give rise to very high derivatives:
The objective function for highly nonlinear deep neural networks or for recurrent neural networks often contains sharp nonlinearities in parameter space resulting from the multiplication of several parameters. These nonlinearities give rise to very high derivatives in some places. When the parameters get close to such a cliff region, a gradient descent update can catapult the parameters very far, possibly losing most of the optimization work that has been done.