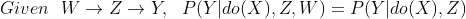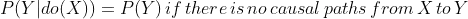4

I'm reading Judea Pearl's "Book of Why" and although I find it really interesting (and potentially useful) I find the lack of explicit equations difficult to deal with. I want to know if I'm getting the back-door adjustment formula correct.

I understand that process for getting the list of confounders using the back-door criteria. So let's say I want to understand the effect of $X$ on $Y$ and I have a single confounder $Z$. As I understand it, the formulas are (assuming all the variables are binary):

$Pr[X|do(Y)] = Pr[X=1|Y=1,Z=0] \times Pr[Z=0] + Pr[X=1|Y=1,Z=1] \times Pr[Z=1]$

$Pr[X|do(!Y)] = Pr[X=1|Y=0,Z=0] \times Pr[Z=0] + Pr[X=1|Y=0,Z=1] \times Pr[Z=1]$

and the "effect" of $Y$ on $X$

$Pr[X|do(Y)] - Pr[X|do(!Y)]$

Are these correct? Also, which one is referred to as the "back-door adjustment formula"?

roundsquare
  • 700
  • 3
  • 13
  • 1
    Weird... it seem like using the tilda in latex doesn't work. I replace them with ! to mean "not". – roundsquare Sep 06 '18 at 15:39
  • `$\tilde{x}$` gives $\tilde{x}$ – Alexis Sep 06 '18 at 16:00
  • Thanks! Do you know how to put the tilda before the variable? I think its easier to read. – roundsquare Sep 06 '18 at 16:03
  • For a more in-depth-but-still-introductory book, I would highly recommend *Causal Inference in Statistics: A Primer*, by Pearl, Glymour, and Jewell. It gets you to the point where you can do serious calculations, without being as academic as *Causality: Models, Reasoning, and Inference*, by Pearl. That last would be a good one to hammer down your understanding, but it is a much denser book, and doesn't have exercises. – Adrian Keister Apr 17 '20 at 14:53
  • 1
    Thanks @AdrianKeister. I ended up getting that book a little while ago and going through it. You are right, it was at the level I needed! – roundsquare Apr 17 '20 at 17:21
  • $\texttt{\sim x}$ gives $\sim x$. – Peter Leopold Aug 29 '20 at 01:14

2 Answers2

2

I found the answer later in the book (equation 7.2). As stated there:

$Pr[Y|do(X)]=\sum_z(Pr[Y|X,Z=z] \times Pr[Z=z])$

which is the same as the formulas posted above (and, as far as I can tell, this is the "back-door adjustment formula").

roundsquare
  • 700
  • 3
  • 13
1

The formula for back-door adjustment given above is correct.

Derivations of the back-door and front-door adjustment formulas rely on the following do-calculas operations summarized below.

Rule #1

formula

Rule #2

formula

Rule #3

formula

I would recommend the reader read a previously answered post by Carlos Cinelli for a good understanding of how they can be used to derive both adjustments for a post-interventional distribution using only observational data.

Pearl Causal Hierarchy (PCH) theorem defines the ladder of causation. If we are successful in removing the do-operations, then we can use associational (L1) data for inferring the causal effect (L2).

Yuri Plotkin
  • 41
  • 1