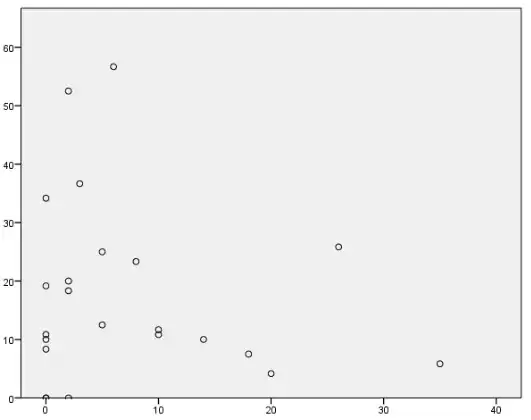
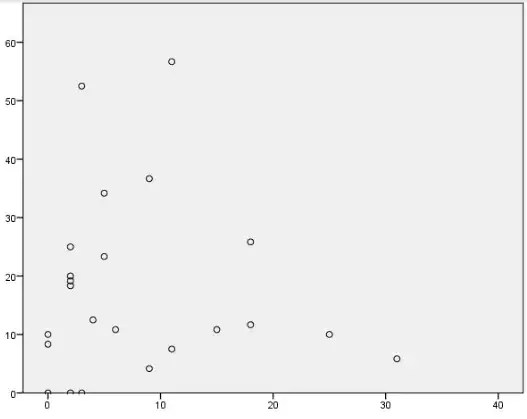
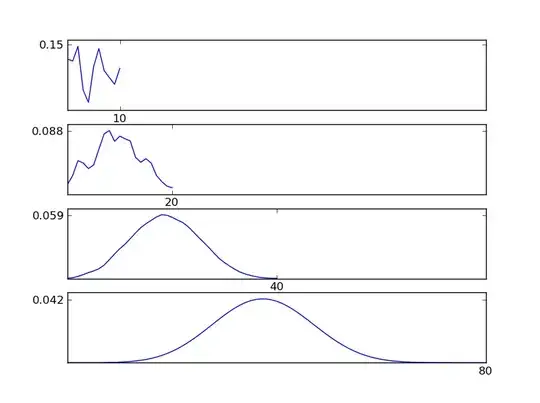
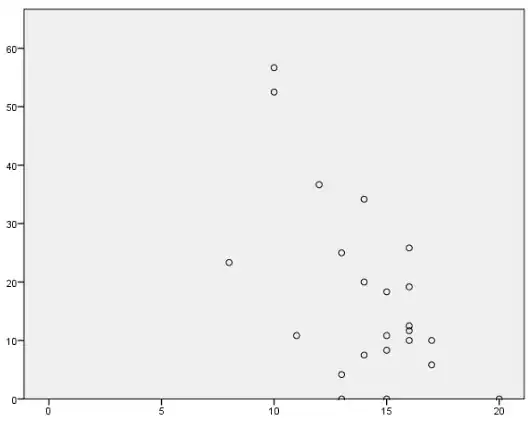
I performed a linear regression which came out with a significant result however when I checked the scatter-plot for linearity I was not confident that the data was linear.
Are there any other ways to test for linearity without inspecting the scatterplot?
Could the linear regression be significant if it wasn't linear?
[Edited to include scatterplots]