Example 1: $\eta(k)$ is constant, and $\underset{k\rightarrow\infty}{\text{lim}}\space d=\infty$
Let $f=x^2$.
Then:
$$
\begin{gathered}m=0\\
\nabla f\left(x\right)=2x\\
d\left(k+1\right)=\left|x\left(k+1\right)-m|=|x\left(k\right)-\eta\left(k\right)\nabla f\left(x\left(k\right)\right)-0\right|=\\
\left|x\left(k\right)-\eta\left(k\right)2x\left(k\right)\right|=\left|x\left(k\right)\right|\cdot\left|1-2\eta\left(k\right)\right|=\\
\left|x\left(k\right)-m\right|\cdot\left|1-2\eta\left(k\right)\right|=d\left(k\right)\left|1-2\eta\left(k\right)\right|\\
\downarrow\\
d\left(k+1\right)=d\left(k\right)\left|1-2\eta\left(k\right)\right|
\end{gathered}
$$
Therefore, assuming that $x(0)\not=0$, it holds that $d(k)$ is a geometric progression that converges to $\infty$ for any $\eta>1$.
E.g. for $\eta=1.01$:
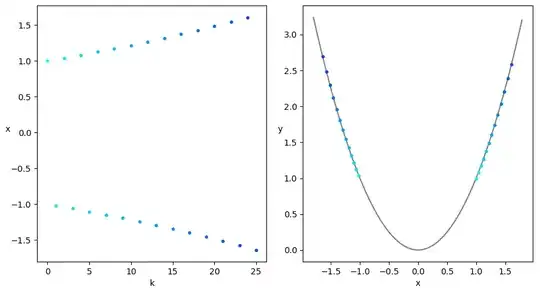(Points get darker as $k$ increases.)
Example 2: $\eta(k)$ is constant, and $\underset{k\rightarrow\infty}{\text{lim}}\space d\not=\infty,0$
Let $f=x^2$.
As shown above, $d\left(k+1\right)=d\left(k\right)\left|1-2\eta\left(k\right)\right|$, so for $\eta=1$, we get $d\left(k+1\right)=d\left(k\right)\left|1-2\right|=d\left(k\right)$, i.e. $d(k)$ is constant, and $x(k)$ is the sequence $x(0), -x(0), x(0), -x(0), ...$
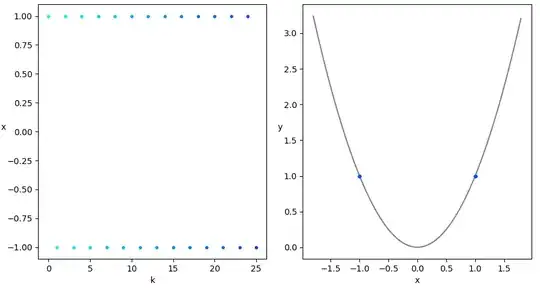
By the way, it is interesting to see that for $\eta=0.5$, the GD converges after a single step for any $x(0)\not=0$.
Example 3: $\underset{k\rightarrow\infty}{\text{lim}}\space \eta (k)=0$ and $\underset{k\rightarrow\infty}{\text{lim}}\space d=\infty$
Let:
- $f=x^4$
- $\eta\left(k\right)=\frac{1}{k+1}$.
- $x(0)=1$
Then: $$\begin{gathered}m=0\\
\nabla f\left(x\right)=4x^{3}\\
d\left(k+1\right)=\left|x\left(k+1\right)-m|=|x\left(k\right)-\eta\left(k\right)\nabla f\left(x\left(k\right)\right)\right|=\\
\left|x\left(k\right)-\eta\left(k\right)4\left(x\left(k\right)\right)^{3}\right|=\left|x\left(k\right)\right|\cdot\left|1-4\eta\left(k\right)\left(x\left(k\right)\right)^{2}\right|=\\
d\left(k\right)\cdot\left|1-4\frac{\left(d\left(k\right)\right)^{2}}{k+1}\right|\\
\downarrow\\
d\left(k+1\right)=d\left(k\right)\cdot\left|1-4\frac{\left(d\left(k\right)\right)^{2}}{k+1}\right|
\end{gathered}
$$
Therefore, if $d(k)\ge k+1$ (which also means that $d(k)\ge 1$), then:
$$\begin{gathered}
\frac{\left(d\left(k\right)\right)^{2}}{k+1}\ge1\\
\downarrow\\
\left|1-4\frac{\left(d\left(k\right)\right)^{2}}{k+1}\right|\ge3\\
\downarrow\\
d\left(k+1\right)\ge3d\left(k\right)
\end{gathered}
$$
and also:
$$\begin{gathered}d\left(k+1\right)\ge3d\left(k\right)\ge3\left(k+1\right)\ge k+2\\
\downarrow\\
d\left(k+1\right)\ge k+2
\end{gathered}
$$
We chose $x(0)=1$, so $d\left(0\right)\ge0+1$, and we can prove by induction that $d\left(k+1\right)\ge3d\left(k\right)$ for any $k\in\mathbb N$.
Thus, $d(k)$ is a geometric progression that converges to $\infty$.
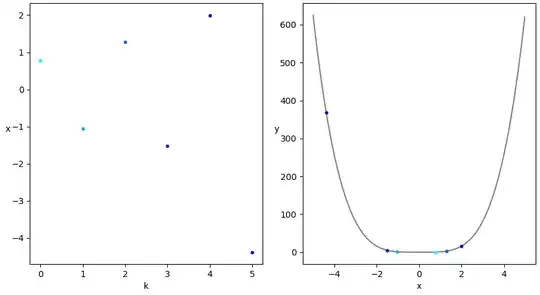($x^4$ is truly a wild function, so the GD explodes so fast that I managed to get a reasonable image for only 6 points, and I had to use $x(0)=0.76945$.)
Here is my code for making the animations, from which the images were taken:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
def f1(x):
return x ** 2
f2 = f1
def f3(x):
try:
return x ** 4
except OverflowError:
print('x is too large... (The growth of x ** 4 is just crazy)\n'
'I am afraid you have to just make INTERVAL bigger, and be '
'satisfied with 3 data points :( ')
exit()
def f1_grad(x):
return 2 * x
f2_grad = f1_grad
def f3_grad(x):
return 4 * x ** 3
func_to_grad_dict = {f1: f1_grad,
f2: f2_grad,
f3: f3_grad}
func_to_sane_range_dict = {f1: (-1.8, 1.8, 0.01),
f2: (-1.8, 1.8, 0.01),
f3: (-5, 5, 0.01)}
func_to_color_diff_dict = {f1: 0.03,
f2: 0.03,
f3: 0.3}
def learning_rate_1(k):
return 1.01
def learning_rate_2(k):
return 1
def learning_rate_3(k):
return 1 / (k + 1)
x0_1 = 1
x0_2 = 1
x0_3 = 0.76945
def plot_func(axe, f):
xs = np.arange(*func_to_sane_range_dict[f])
vf = np.vectorize(f)
ys = vf(xs)
return axe.plot(xs, ys, color='grey')
def next_color(color, f):
color[1] -= func_to_color_diff_dict[f]
color[1] = max(0, color[1])
return color[:]
###########################################
# script parameters
X0 = x0_1
F = f1
LEARNING_RATE = learning_rate_1
INTERVAL = 1
INTERVAL = 3e1
INTERVAL = 9e2
INTERVAL = 3e2
###########################################
k = 0
x = X0
f = F
f_grad = func_to_grad_dict[f]
cur_color = [0, 1, 1]
fig, (k_and_x, x_and_y) = plt.subplots(1, 2, figsize=(9,5))
k_and_x.set_xlabel('k')
k_and_x.set_ylabel('x', rotation=0)
x_and_y.set_xlabel('x')
x_and_y.set_ylabel('y', rotation=0)
plot_func(x_and_y, f)
k_and_x.plot(k, x, '.', color=cur_color[:])
x_and_y.plot(x, f(x), '.', color=cur_color[:])
plt.tight_layout()
def update(frame):
global k, x
gradient = f_grad(x)
x -= LEARNING_RATE(k) * gradient
k += 1
color = next_color(cur_color, f)
print(f'k: {k}\n'
f'x: {x}\n')
k_x_marker, = k_and_x.plot(k, x, '.', color=color)
x_y_marker, = x_and_y.plot(x, f(x), '.', color=color)
return k_x_marker, x_y_marker
ani = FuncAnimation(fig, update, blit=False, repeat=False, interval=INTERVAL)
plt.show()
