Why use parametric test at all if non parametric tests are 'less strict'

Question

I have read from several sources, even in my undergrad courses, that parametric tests require the data to have a certain distribution, for instance normal, whilst non-parametric don't.

I have analyzed several real-life data consisting of thousands of rows. After analyzing them, I have found none of them have any normal distributions, therefore ANOVA, t-tests, chi-Square and other parametric tests that require normal distributions are out of the picture.

I have also shared this normal distribution rarity issue here. It seems it is also generally agreed that normal distribution is rare.

My question is if data with a normal distribution are rare in real life, then won't it mean that parametric tests that require normal distributions, such as ANOVA, t-test, and Chi-Square, are pretty much not used often, i.e. useless?

I am not a statistics student, so please don't use too much mathematics or heavy statistical terms.

Answer 1

It is true that precisely normal populations are rare in the real world.

However, some very useful procedures are 'robust' against mild non-normality. Perhaps the most important of them is the t test, which performs remarkably well with samples of moderate or large size that are not exactly normal.

Also, some tests that were derived for use with normal data have better power than nonparametric alternatives (that is, they are more likely to reject the null hypothesis when it is false), and this advantage persists to an extent when these tests are used with slightly non-normal data.

Nonparametric tests such as sign tests and the rank-based Wilcoxon, Kruskal-Wallis, and Friedman tests lose information when data are reduced to ranks (or to +'s and -'s), and the result can be failure to find a real effect when it is present in experimental data.

You are correct that some ANOVA tests behave badly when data are not normal, but many tests using the chi-squared distribution are for categorical data and normality is not an issue.

Recently, new nonparametric methods of data analysis have been invented and come into common use because computation is cheaper and more convenient now than it was several years ago. Some examples are bootstrapping and permutation tests. Sometimes they require hundreds of thousands or millions of computations compared with dozens for traditional tests. But the extra computation may take only seconds or a few minutes with modern computers.

Admittedly, some statisticians are not familiar with these new methods and fail to take appropriate advantage of them. Also, part of the reluctance to change is that consumers of or clients for statistical analyses may not trust results from procedures they have never heard of. But that is changing over time.

Fortunately, modern software and computers also make it possible to visualize data in ways that were previously tedious to show. As a very simple example (not using very fancy graphics), here are two plots of some data that I know cannot possibly be normal (even though they do manage to pass a couple of tests of normality because of the small sample size.)

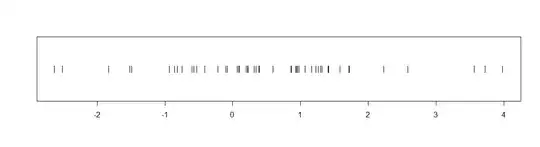
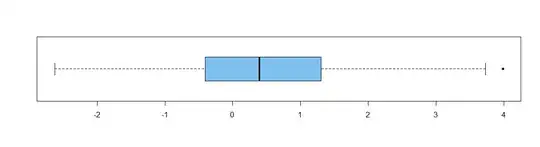
These data are also pretty obviously not centered at $0.$ The optimum statistical procedure to confirm that would not be a t test or even a nonparametric Wilcoxon test. But both of these tests reject the null hypothesis that the data are centered at $0$: the t test with a P-value 0.013, the Wilcoxon test with P-value 0.0099. Both P-values are less than 0.05, so both confirm the obvious at the 5% level.

It is hardly a loss to science if I don't get around to using the optimal test. And some of the people reading my findings might be a lot more comfortable having the results of a t test. Maybe the next generation of clients will be more demanding.

Answer 2

Tests such as t-tests don't actually require the data to be normal. What they require is that the distribution of the sample mean of the data (under the null hypothesis) follows a normal distribution (or very close to it). This will cause the t-statistic to follow a t-distribution, as it should. This happens when the data is normal, but also frequently when the data is not normal, as long as the sample size is moderately large. This is a consequence of the central limit theorem. Try this: make some fake non-normal data. This will represent your population. Repeatedly draw a sample of a large size from this data, and calculate its sample mean. Plot all of these sample means and you will see that they look normal. You can also plot all of the t-statistics and you will see that they look like they follow a t-distribution.

Answer 3

All computation is based on model building. When you count two apples you imply, that there are either two identical things or a precise definition of what an apple exactly is and on what an apple exactly not is. The truth is: There is no sharp and precise definition of what an apple is, but our usual feeling, whether something is an apple, is "precise" enough.

An ANOVA or a t-test needs the distribution to be perfectly normal in order to produce a perfectly true p-value. However, nobody is in need of a p-value to be exact to the 10th digit. Never!

So the question boils down to the question, when is a distribution "close enough to normal" and fact is, many distributions are "close enough" to make parametric tests worthwile learning and using.

Parametric tests perform very well when you need an easy to understand effect measure like Cohen's d or when you are in need of a power calculation.

That being said, there will probably be a trend away from classical tests to computationally involving tests. However, for the foreseeable future, linear regression will always come with a t-test for each predictor and when you compute Bravais-Pearson correlation, standard computer programs will test that using the t-distribution. Right now, parametric tests are dominant.

Answer 4

I think I can summarise the other answers as follows: in many non-normal cases (if the breach of normality is not too big), parametric tests still have good power, while (important!) the actual type I-error rate is close to the nominal $\alpha$-level, so why not use them?

I would like to add that parametric tests offer the huge advantage of providing an estimate of the effect size, while Wilcoxon etc. only offer p-values.