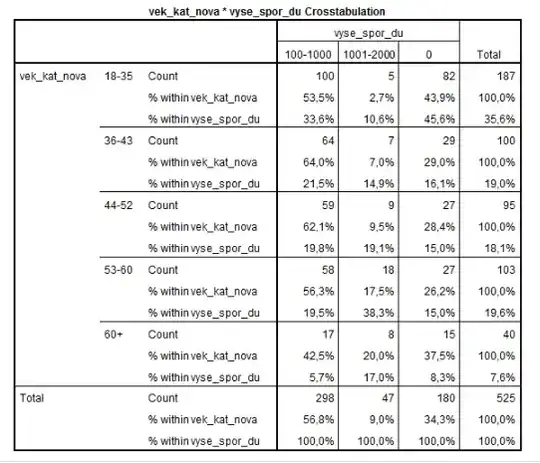
I have two ordinal variables. I would like to know if there is a dependency between these two variables and also how strong this dependency is. So, I performed a chi-square test (34.53, df=8) where the p-value < 0.05. No problem here.
Then because these two variables are ordinal I choose gamma and Somers' d to show how strong the dependency is. The problem is that both Somers' d (-0.036) and gamma (-0.056) show no statistical significance p-value for both 0.345.
I don't know how to interpret these results: there is statistical significance in dependency (chi-square) and also no statistical significance in the strength of this dependency ?