I am calculating a tolerance interval following http://www.itl.nist.gov/div898/handbook/prc/section2/prc253.htm but this says to multiply the k value by the standard deviation of the sample. I have a model with a fit line, so I would think I do not want to use the standard deviation, but rather some value that reflects the residuals, and instead of using the sample mean, I will use the predicted value from my linear regression model. Is that right? What value do I use instead of the standard deviation?
I could (maybe should have) asked the question this way: Given a linear model, how do I compute a one-sided tolerance interval. I think a tolerance interval is the right thing for my problem based on this: http://www.kmjn.org/notes/tolerance_intervals.html
Edit again: I found this formula for "Assuming linear function and no replicates, the standard deviation about the regression" (from here)
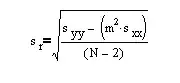
Is this the right fomula to get a value to multiply by the k values?