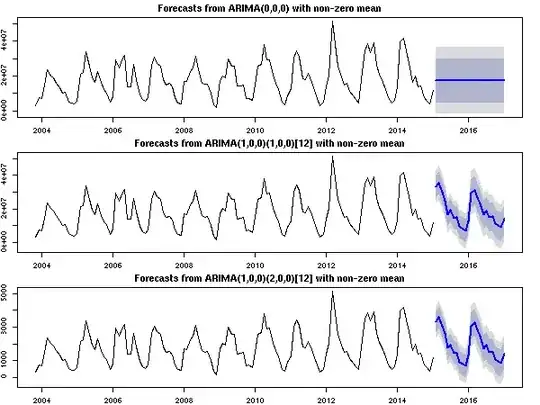
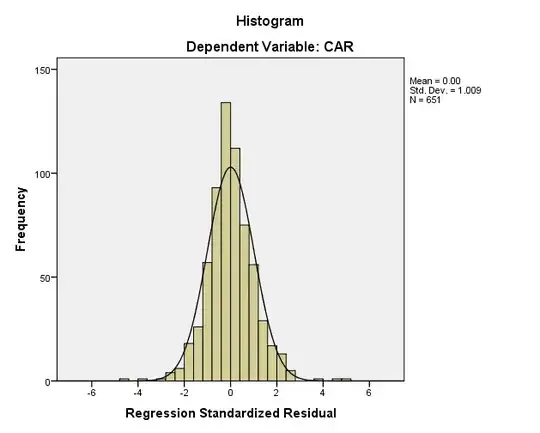
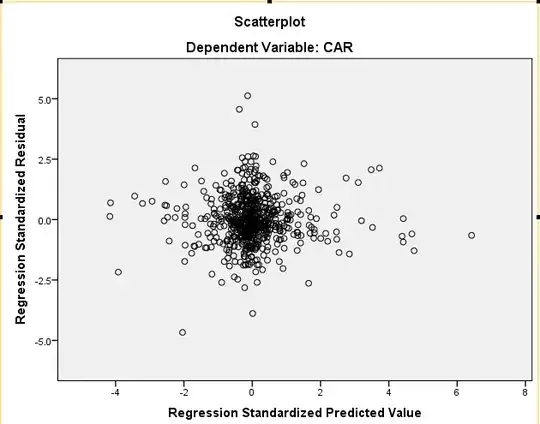
I searched online and looked video tutorials but I'm still not sure. Would you consider the below data normally distributed? I know the ideal fit in theory would be that most of the points are on the line. However data in the real world can be different. So would like to hear your opinion from a practical point of view. Would it be safe to perform a regression analysis on this dataset?
--------------------UPDATED INFORMATION------------------------
Skewness .291 Excess Kurtosis 2.489
Both Shapiro and Kolmogorov show significance at .000 level (therefore not normal)