Difference between random effect and fixed effect with regularization/prior

Question

Let's say I have a random effect intercept. For example:

lme4::lmer(yield ~ 1 + (1|Batch))

How is that different than just ordinary regression using regularization or a prior?

 arm::bayesglm(yield ~ 1 + Batch,...)

They seem roughly equivalent to me.

Addendum

Unified view on shrinkage: what is the relation (if any) between Stein's paradox, ridge regression, and random effects in mixed models? asks something similar. The accepted answer claims that they are equivalent.

However, I am not convinced that it is correct, otherwise what is the need for a package lme4, which is typically more computationally expensive to fit?

My intuition is that regularization is equivalent to a mixed model with a diagonal covariance matrix for the random effects. Whereas something like lme4 supports more general covariance structures.

Possible duplicate of [Unified view on shrinkage: what is the relation (if any) between Stein's paradox, ridge regression, and random effects in mixed models?](https://stats.stackexchange.com/questions/122062/unified-view-on-shrinkage-what-is-the-relation-if-any-between-steins-paradox) — amoeba, Aug 18 '18 at 12:12
@amoeba I am not convinced that the answer there is correct. See the addendum to my question. — Jeff, Aug 18 '18 at 18:06
part of the difference is that mixed models are simultaneously estimating the appropriate degree of shrinkage (under the assumption that the random effects are Normally distributed). e.g. for `bayesglm` you have to specify the prior on the fixed effects. — Ben Bolker, Aug 18 '18 at 21:17
I think the answer there is correct, but of course it does not imply that the whole `lme4` is just equivalent to ridge regression. lme4 can estimate very complicated covariance structures; but your example with one random intercept term is indeed very similar to having a L2 penalty (or prior), as explained in the linked answer. It's true what @BenBolker wrote though; it's more like empirical Bayes, where the prior is estimated from the data (or like ridge regression when the penalty is optimized over). — amoeba, Aug 18 '18 at 21:58
My question was more broader. I guess the example I provided is too simple. I was trying to get at the heart of what could be modeled with a mixed model that can't be accomplished with simpler approaches, e.g., bayesglm. For me this has practical considerations, as I am looking at modeling things that are possibly too expensive with lme4. — Jeff, Aug 18 '18 at 22:02
BTW, I agree that Ben's answer is an important distinction. If it is the only distinction between the two then I will consider that the answer. — Jeff, Aug 18 '18 at 23:34
@Ben-Bolker would you like to provide an answer? If I don't get any other responses, I will just craft answer based on your comment. — Jeff, Aug 20 '18 at 17:54

Phil Assheton · Answer 1 · 2021-05-01T22:08:06.647

A couple of years too late, but I'd really like to add my own intuitions on this topic. It's my own take, so if I'm wrong about this, please do pull me up.

As Ben says in the comments, the main difference is that the mixed model estimates the right amount of shrinkage for you. But you might want to understand this more deeply (as I did)...

The main hurdle we need to get over is to understand exactly what the mixed model is doing when it shrinks the coefficients, and why. For me the clearest intuition about random effect shrinkage is: shrinkage is an attempt to reverse the effects of adding noise.

The Effects of Adding Noise

It's often easier to understand stats if we make a sillily-exaggerated example. In that spirit, have a look at the graph below (I have added the code at the bottom of this answer, in case you want to have a play with it).

Here we have twelve groups. The true group means are in red: they are normally distributed with a standard deviation of 1. The grey dots are samples drawn from these groups; within each group, there is a lot of noise: with a standard deviation of 5. For groups 1 to 6, we have 100 samples from each group. For groups 7 to 12, only two each. The blue crosshairs are our attempts at hitting the red targets: they are the means of the samples from the groups.

Now, here's the key intuition that justifies shrinkage: noise makes things spread out. (And shrinkage is simply the reversal of this.)

We can see that particularly clearly in groups 7-12, where the crosshairs are scattered quite widely compared with the red targets. We can calculate how spread out these are using two facts from basic 101 stats:

Firstly, we know that the variance of a sum is the sum of the variances.
The variance of a sample mean is the variance of the individual data-points divided by the number of datapoints.

So, the variance of our crosshairs is

$\mathrm{var}(crosshairs_i) = \mathrm{var}(red\_dots) + \mathrm{var}(within\_sample)/n_i = 1^2 + 5^2/n_i$

where $n_i$ is the sample size in the group we are concerned with, group $i$. (We know that $\mathrm{var}(crosshairs)$ differs between the groups; just look at the graph!)

So, for groups 1 to 6 that means var(crosshairs) = 1.25, and for groups 7 to 12, var(crosshairs) = 13.5. In the latter case, the crosshairs are truly terrible estimates for the red dots -- they are $SD=\sqrt{13.5}=3.7$ times as spread out as they should be. BUT note that they are also not exactly perfect in groups 1 to 6 either, having $\sqrt{1.25} = 1.12$ times the spread that they should.

The Solution: Shrinkage

So, the idea of shrinkage is: let's try to bring them into the right ballpark. We'll harness all the data in all the groups to try to estimate the overall grand mean (the mean of all the red dots) and shrink all our data points towards that, according to how far they will likely have been thrown out by the noise. In the end, we hope to give them the same variance as the red dots. We can do that by dividing by the $\sqrt{\mathrm{var}(crosshairs)}$, and multiplying by $\sqrt{\mathrm{var}(red\_dots)}$, so that they will have the right variance.

(Of course, we don't know var(red_dots) or var(within_sample), but conveniently, our mixed model can estimate those for us -- and, again, it can pool all of the data together to get that as accurate as possible).

So, in the example above, if we shrink all the blue crosses towards towards the grand mean we are able to pool all the available information (both in estimating the grand mean, and in estimating the red_dots and within_sample variances) and use those to pull the crosshairs back to the zone where they should have been in the first place. Now, for groups 7 to 12, it's probably a bit late for them: those means are dominated by that noise, so the best we can do is to pull them back so that they are not pathologically far off. For means 1 to 6 though, they are dragged in, just a little bit, and that little bit, just like with the other ones, will get them that little bit closer to where they are meant to be.

The purple crosses above show the result of doing this (compared with the blue crosses that were our original estimates). We can see that by pooling the information together we've been able to use information from the larger groups to place the smaller groups in a much more sensible position. But this is important: it is not only that the small groups learn from the big ones. They all learn from each other. All of them need to be pulled in, even if just a little bit, and they use the information that is pooled between all of them to do that.

Comparison to Bayes

I should say that Bayesian stuff isn't my area. But this has been a really nice opportunity to try my first experiments in the area, and the results are really interesting. Remember that the mixed model is trying to reduce the variance of the estimated means so that they will have what it estimates to be the "right" variance. In this case, it estimates the groups to have a SD of 0.75 and the within_group SD to be 5.1. It estimates the grand mean to be 0.035.

The Bayesian method is rather similar, but you get to choose your own grand mean and SD to aim for! But, if we build our prior based on the mixed model, that is, if we set our prior to be normal with mean 0.035 and SD 0.75, look what happens:

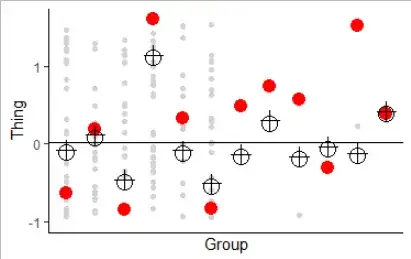
Here, the crosses are the predicted effects from lme4; the black circles are the parameter estimates from bayesglm... (The red dots are as before). Spooky eh?

Can I Just Use bayesglm Instead of lmer?

The bad news, if (as per your comments) you're looking to shortcut by using bayesglm, is that it is that step -- estimating the variances in the mixed model -- that is the computationally expensive bit. (And lme4 is already pretty smart about how it reduces that). So, you're kinda back to square one.

Code

library(ggplot2)
library(lme4)
library(arm)


group.sizes <- c(100, 100, 100, 100, 100, 100, 2, 2, 2, 2, 2, 2)
between.group.sd <- 1
within.group.sd <- 5


set.seed(1)


# simulate data
num.groups <- length(group.sizes)
u <- rnorm(num.groups, sd=between.group.sd)
sample.data <- data.frame(
  group.num = unlist(mapply(rep,   times=group.sizes, x=1:num.groups)),
  samples   = unlist(mapply(rnorm, n    =group.sizes, mean=u, sd=within.group.sd))
)

# estimate means
means <- data.frame(
  group.num   = 1:num.groups,
  true.mean   = u,
  sample.mean = with(sample.data, aggregate(samples, by=list(group.num), FUN=mean))$x
)
grand.mean <- mean(sample.data$samples)

# fit a mixed model
mixed.model <- lmer(samples~(1|group.num), data = sample.data)

# use estimate from mixed model to fit a bayesglm
mixed.model.u.sd <- sqrt(as.numeric(VarCorr(mixed.model)$group.num))
mixed.model.int  <- fixef(mixed.model)
bayes.model <- bayesglm(
  samples~factor(group.num)+0, 
  data=sample.data, 
  prior.mean=mixed.model.int, 
  prior.scale=mixed.model.u.sd, 
  prior.df=Inf, 
  scaled=FALSE
)

# pull the different mean estimates from the different models
means$bayesian       <- coef(bayes.model)
means$random.effects <- ranef(mixed.model)[["group.num"]][["(Intercept)"]]
means$shrunken.mean  <- grand.mean + 
  (means$sample.mean - grand.mean) / sqrt(between.group.sd^2 + within.group.sd^2 / group.sizes)

# so we can zoom the graphs in
red.dot.lims <- c(
  min(means$true.mean),
  max(means$true.mean)
)
crosshairs.lims <- c(
  min(means$sample.mean),
  max(means$sample.mean)
)


plot.with.sample.means <- ggplot(means, aes(group.num)) +
  geom_point(aes(y=samples),              size=1.5, colour="light grey", data=sample.data) +
  geom_point(aes(y=true.mean),            size=4,   colour="red"                         ) +
  geom_point(aes(y=sample.mean), shape=4, size=4,   colour="blue"                        ) +
  scale_y_continuous("Thing") +
  scale_x_discrete("Group") +
  theme_classic()

print(plot.with.sample.means)

plot.with.shrunken.means <- ggplot(means, aes(group.num)) +
  geom_point(aes(y=samples),                size=1.5, colour="light grey", data=sample.data) +
  geom_point(aes(y=true.mean),              size=4,   colour="red"                         ) +
  geom_point(aes(y=sample.mean),   shape=4, size=4,   colour="blue"                        ) +
  geom_point(aes(y=shrunken.mean), shape=4, size=4,   colour="magenta"                     ) +
  scale_y_continuous("Thing", limits = crosshairs.lims) +
  geom_hline(yintercept=grand.mean) +
  scale_x_discrete("Group") +
  theme_classic()

print(plot.with.shrunken.means)

plot.mixed.model.vs.bayes <- ggplot(means, aes(group.num)) +
  geom_point(aes(y=samples),                 size=1.5, colour="light grey", data=sample.data) +
  geom_point(aes(y=true.mean),               size=4,   colour="red") +
  geom_point(aes(y=bayesian),       shape=3, size=4,   colour="black") +
  geom_point(aes(y=random.effects), shape=1, size=5,   colour="black") +
  scale_y_continuous("Thing", limits = red.dot.lims) +
  geom_hline(yintercept=grand.mean) +
  scale_x_discrete("Group") +
  theme_classic()

print(plot.mixed.model.vs.bayes)