I have been trying to estimate the marginal posterior for D variable using Laplace approximation:
$p(\theta_i) \approx \left[\frac{\det{H}}{2\pi\det{H(\theta_i)}}\right]^{1/2} \exp\left[-L(\theta_i, \psi_i^*) + L(\theta^*)\right]$
which can be simplified to:
$p(\theta_i) \approx C \left[\det{H(\theta_i)}\right]^{-1/2} \exp\left[-L(\theta_i, \psi_i^*) \right]$
where $\theta_i$ is the parameter of interest, $H(\theta_i)$ is the $D-1 \times D-1$ Hessian about the maximum a posteriori (MAP) $\psi_i^*$ and $L(\theta_i, \psi_i^*)$ is the negative log posteriori (log-likelihood + log prior).
My negative log posteriori is made of a log-likelihood:
$l(vars|x) = \frac{\sum\limits_{i=1}^n (x_i-y_i(var1, var2, var3))^2}{ 2 \sigma_i(var 4)^2}$
where $y_i(var1, var2, var3) = (var 2 * ts1 + var 3 * ts2 + ts3)/var1$
t1, ts2 and ts3 are three different time series of measurements.
and $\sigma_i(var 4) = \sqrt{var 4 *x_i^2}$
which is a normal distribution of the residuals centered in 0. The predictions depends on the three first variables, while the standard deviation depends on var 4.
To get the log-posteriori four priors are used:
a uniform distribution (between 0.5 and 1) is used for var 1
two Weibull distribution for var 2 and 3
An inverse gamma distribution for var 4
Some of my variables are constrained so I have been using the L-BFGS-B algorithm to find the maximum a posteriori and an approximation of the Hessian.
Unfortunately, the results are not so good particularly the Hessian approximation.
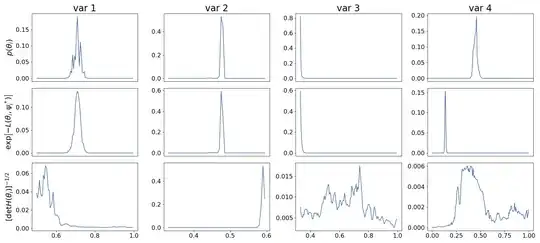
On the graph you can see the marginal posteriori on the first row, the posteriori on the second row and the squared root of the determinant of the inversed Hessian on the third row. These results are for four different variables (different columns).
The determinant of the Hessian seems to create a lot of fluctuations in the marginal posteriori. I believed it is because L-BFGS-B gives only an approximation of the Hessian matrix that do not seem so accurate. As the Hessian matrix is not calculated anew at every iteration but is simply updated using the secant equation. I tried to assess how precise was the estimation of the Hessian by changing the starting values of the algorithm. Indeed, in my opininion if the update of the Hessian matrix at every step is a good approximation it should be relatively independent from the path from the starting values to the optimized point. However, I found that if I changed the starting values, the algorithm still converged to the same maximum but the determinant of the Hessian changed by a factor as high as $10^2$.
I'm wondering if you had any advices concerning the choice of the optimizing algorithm and the method to get the estimated Hessian matrix. Possibly a fast method as I have to do that analysis an important number of times.
Note: I also tried Nelder-Mead with a quadratic barrier contraints but it was too slow and the estimation of the Hessian matrix was also impacted by the quadratic loss near the boundaries.
Thank you for your time!