Sometimes it appears that the covariance is not sufficient to express how much two random variables are related.
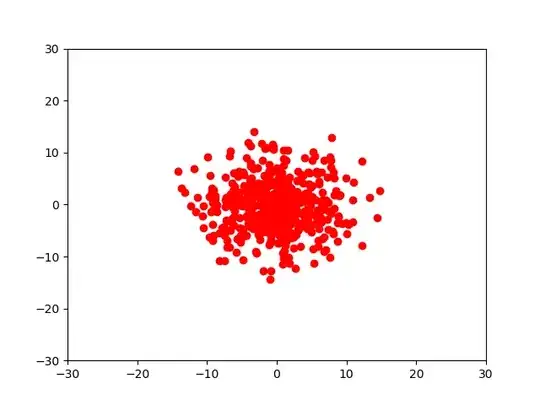
Bellow, I have draw random samples from a multivariate normal distribution with two random variables X and Y.
First case : Cov(X,Y) $\simeq$ 0
Second case : Cor(X,Y) $\simeq$ 1

Third case: Cor(X,Y) $\simeq$ 0, ok but then is there a better metric than correlation in this case ?
Remark : Here the python code to draw the examples :
import numpy as np
import matplotlib.pyplot as plt
s1 = np.random.normal(0, 5, 500)
s2 = np.random.normal(0, 1, 500)
f, axarr = plt.subplots(2, 2)
axarr[0, 0].scatter(s1, s2)
axarr[0, 0].set_title('X,Y ')
axarr[0, 1].scatter(s1, s1+s1)
axarr[0, 1].set_title('X, X+X')
axarr[1, 0].scatter(s1, s1*s1)
axarr[1, 0].set_title('X,X*X')
axarr[1, 1].scatter(s1, s1+s2)
axarr[1, 1].set_title('X,X+Y')
plt.show()