Suppose there is a left-censored normal distribution, and we know there is a total of $m$ samples, for which we know $n$ of them. I am trying to estimate the mean and variance of the underlying normal distribution. I find the maximum likelihood estimator by maximizing $\sum_i^n log(p(x_i|\mu,\sigma^2)$, where $p$ is the pdf of $N(\mu,\sigma^2 )$ at $x_i$ (using numerical methods)
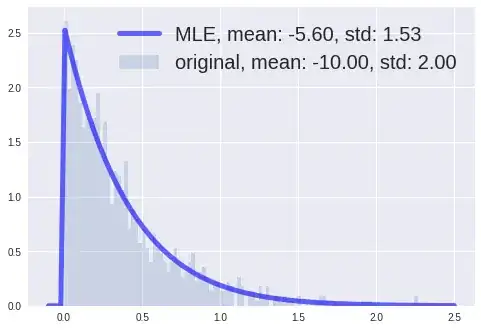
When i do the simulation, the mle does not match exactly the true one, but it can fit quite well to the samples in some cases:
But the problem is that when the distance of mean from zero is too large comparing to the variance/ std, the optimization messed up and does not give a good result. I read somewhere that it is related to the convergence of the MLE but i forgot where. Can someone explain why or have suggestion on improving the estimation?
I have also read another post and it is mentioned that its maximum likelihood approach may be unstable if more than half of data is censored, but i still want to give it a try. However, i don't understand the $F$ term mentioned in that post, is it the cdf at 0 for the setting here? Why do we have such term when we only know there is $m-n$ samples but nothing more in the censored region?