What is the difference between the Shapiro–Wilk test of normality and the Kolmogorov–Smirnov test of normality? When will results from these two methods differ?
2 Answers
You can't really even compare the two since the Kolmogorov-Smirnov is for a completely specified distribution (so if you're testing normality, you must specify the mean and variance; they can't be estimated from the data*), while the Shapiro-Wilk is for normality, with unspecified mean and variance.
* you also can't standardize by using estimated parameters and test for standard normal; that's actually the same thing.
One way to compare would be to supplement the Shapiro-Wilk with a test for specified mean and variance in a normal (combining the tests in some manner), or by having the KS tables adjusted for the parameter estimation (but then it's no longer distribution-free).
There is such a test (equivalent to the Kolmogorov-Smirnov with estimated parameters) - the Lilliefors test; the normality-test version could be validly compared to the Shapiro-Wilk (and will generally have lower power). More competitive is the Anderson-Darling test (which must also be adjusted for parameter estimation for a comparison to be valid).
As for what they test - the KS test (and the Lilliefors) looks at the largest difference between the empirical CDF and the specified distribution, while the Shapiro Wilk effectively compares two estimates of variance; the closely related Shapiro-Francia can be regarded as a monotonic function of the squared correlation in a Q-Q plot; if I recall correctly, the Shapiro-Wilk also takes into account covariances between the order statistics.
Edited to add: While the Shapiro-Wilk nearly always beats the Lilliefors test on alternatives of interest, an example where it doesn't is the $t_{30}$ in medium-large samples ($n>60$-ish). There the Lilliefors has higher power.
[It should be kept in mind that there are many more tests for normality that are available than these.]
- 257,508
- 32
- 553
- 939
-
This is an interesting answer, but I am having a little trouble understanding how to square it with practice. Maybe these should be different questions, but what is the consequence of ignoring the parameter estimation in the K-S test? Does this imply that the Lillefors test has less power than an incorrectly conducted K-S in which the pareters were estimated from the data? – russellpierce Nov 13 '13 at 20:42
-
@rpierce - The main impact of treating estimated parameters as known is to dramatically lower the actual significance level (and hence the power curve) from what it should be if you take account of it (as the Lilliefors does). That is, the Lilliefors is the K-S 'done right' for parameter estimation and it has substantially better power than the KS. On the other hand, the Lilliefors has much worse power than say the Shapiro-Wilk test. In short, the KS isn't an especially powerful test to start with, and we make it worse by ignoring that we're doing parameter estimation. – Glen_b Nov 13 '13 at 22:11
-
... keeping in mind when we say 'better power' and 'worse power' that we're generally referring to power against what people generally regard as interesting sorts of alternatives. – Glen_b Nov 13 '13 at 22:18
-
Just to clarify, what you mean is that the SW is more sensitive to departures from normality than the KS (even though the KS shouldn't be used in this way) and the KS is more sensitive than the Lillefors to departures from normality? – russellpierce Nov 27 '13 at 13:46
-
How do you get the second conclusion? Now I'm worried I have misspoken somewhere. – Glen_b Nov 27 '13 at 17:33
-
I suppose I made a bad assumption. Usually estimating extra parameters seems to result in a penalty to power and so I assumed that since the Lillefors was going to estimate the parameters used rather than being handed them by the user (the way a incorrectly performed KS test would), that Lillefors would be less powerful (less able to reject the H0 that the distribution is normal) than KS. – russellpierce Nov 27 '13 at 21:54
-
One problem the KS has is that when you estimate parameters you reduce its type I error rate (far) below the nominal rate. I mentioned this in the first sentence of my first comment following your question. Stepping away from goodness of fit for a moment, have you ever seen a power curve, like one for a t-test? – Glen_b Nov 27 '13 at 22:04
-
I didn't follow what you were saying initially. I now understand that you mean that the p resulting from the KS is 'actually' quite a bit higher than it reports back in cases where you've estimated its parameters. Consequently one is left retaining the null when one really should have rejected it. Yes? – russellpierce Nov 27 '13 at 22:20
-
1I've seen a power curve;I just didn't think through what a lowering or raising of it would mean and instead god stuck on about your second comment starting: "keeping in mind". Somehow I got twisted around and thought you were saying that 'better' power meant having the power curve where it 'ought' to be. That perhaps we were cheating and getting unrealistic power in the KS because we were handing it parameters that it should have been penalized for estimating (because that is what I am used to as a consequence for failing to acknowledge that a parameter comes from an estimate). – russellpierce Nov 27 '13 at 22:23
-
1Not sure how I missed these comments before, but yes, calculated p-values from using the KS test with estimated parameters as if they were known/specified will tend to be too high. Try it in R: `hist(replicate(1000,ks.test(scale(rnorm(x)),pnorm)$p.value))` -- if the p-values were as they should be, that would look uniform! – Glen_b Dec 04 '18 at 23:16
-
Gleb_b I am not sure I buy that K-S has to be for "a" normal distribution with specified mean and variance since we can standardize any normally distributed distribution, yeah? Therefore, why isn't a one sample K-S test of a standardized sample against the $z$ distribution not a general test of normality irrespective of mean and standard deviation? Is it because the standardization would be done with $\bar{x}$ and $s_{x}$ instead of $\mu_{x}$ and $\sigma_{x}$? – Alexis Jan 08 '22 at 19:55
-
1You have exactly the right thought at the end there. You can standardize *if you know the population mean and variance*. If you estimate either or both from the sample, that substantially alters the distribution of the test statistic (try it! code is above). Hence Lilliefors' papers in the 60s on the KS tests with estimation for the case of the normal (estimating $\mu$, estimating $\sigma$, estimating both) and also for the exponential (the test is no longer distribution-free, you have to do it for each specific case). – Glen_b Jan 09 '22 at 01:37
-
1Actually that code won't do what you need, since x isn't defined there. Try: `n=30;hist(replicate(10000,ks.test(scale(rnorm(n)),pnorm)$p.value),n=100)` ... unless you account for the effect of estimation, the test is highly conservative. (This code takes a few seconds to run) – Glen_b Jan 09 '22 at 01:47
-
1Note that I addressed the issue with standardizing in my answer (that it's the same as just specifying the sample statistics as the population statistics). – Glen_b Jan 09 '22 at 01:58
Briefly stated, the Shapiro-Wilk test is a specific test for normality, whereas the method used by Kolmogorov-Smirnov test is more general, but less powerful (meaning it correctly rejects the null hypothesis of normality less often). Both statistics take normality as the null and establishes a test statistic based on the sample, but how they do so is different from one another in ways that make them more or less sensitive to features of normal distributions.
How exactly W (the test statistic for Shapiro-Wilk) is calculated is a bit involved, but conceptually, it involves arraying the sample values by size and measuring fit against expected means, variances and covariances. These multiple comparisons against normality, as I understand it, give the test more power than the the Kolmogorov-Smirnov test, which is one way in which they may differ.
By contrast, the Kolmogorov-Smirnov test for normality is derived from a general approach for assessing goodness of fit by comparing the expected cumulative distribution against the empirical cumulative distribution, vis:
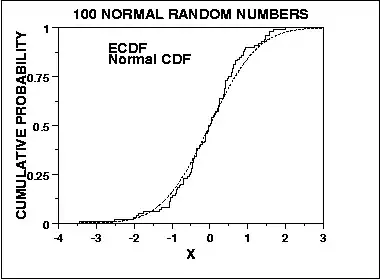
As such, it is sensitive at the center of the distribution, and not the tails. However, the K-S is test is convergent, in the sense that as n tends to infinity, the test converges to the true answer in probability (I believe that Glivenko-Cantelli Theorem applies here, but someone may correct me). These are two more ways in which these two tests might differ in their evaluation of normality.
- 700
- 1
- 9
- 18
- 3,207
- 19
- 16
-
3Besides... Shapiro-Wilk's test is often used when estimating departures from normality in small samples. Great answer, John! Thanks. – aL3xa Jul 30 '10 at 01:24
-
+1, two other notes about KS: it can be used to test against any major distribution (whereas SW is *only* for normality), & the lower power [could](http://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless) be a good thing w/ larger samples. – gung - Reinstate Monica Jul 26 '12 at 16:49
-
How is lower power a good thing? As long as Type I remains the same isn't higher power always better? Furthermore, KS is not generally less powerful, only maybe to leptokurtosis? For example, KS is much more powerful for skew without a commensurate increase in Type 1 errors. – John Nov 24 '12 at 09:14
-
The Kolmogorov-Smirnov is for a fully specified distribution. The Shapiro Wilk is not. They can't be compared ... because as soon as you make the adjustments required to make them comparable, *you no longer have one or the other test*. – Glen_b Nov 08 '13 at 08:18
-
Found this simulation study, in case that adds anything useful in the way of details. Same general conclusion as above: the Shapiro-Wilk test is more sensitive. http://www.ukm.my/jsm/pdf_files/SM-PDF-40-6-2011/15%20NorAishah.pdf – Nick Stauner Nov 08 '13 at 16:01