Testing Hypothesis with Time series and Location Data

Question

I have Data on Prices of house. Along with these variables.

• 1) Location

   i)Latitude-Longitude
   ii)City and State 
  

  2) Attribute of house.

  i) No. of bedrooms and bathrooms (could be taken as proxy for size?)
  

  3)Year Built and prices of house on the same year. (so basically i have price of house when it was built hence time series data)

Now, I want to test the effect of this variables on price individually and combined.

What statistics Can be used for such test? Say, have prices increased in last 3-4 years?

How exactly I can use the lat-long (since this is more granular than just cities) of data to check whether prices of house are dependent on location?

Looking for some suggestions.

Answer 1

How exactly I can use the lat-long (since this is more granular than just cities) of data to check whether prices of house are dependent on location?

Rather than using the latitude and longitude variables directly in your model, it is better to use these variables indirectly in combination with geospacial data on the characteristics of different locations. In most countries there are statistical agencies that publish geospacial maps of 'statistical areas' that are used in survey/census work. The maps show the coordinate boundaries of these areas, which allows you to map each house to a particular statistical area and then extract publicly available variables relating to that statistical area (e.g., measures of socio-economic level, crime level, etc.). This could potentially give you a number of useful variables that are related to house prices. Another thing you may be able to do is to measure the distance from your coordinates to nearby facilities (e.g., distance to nearest school, nearest shop, nearest bus stop, etc.). This can also be done using geospacial maps.

This kind of analysis requires a lot of work, and it is not easy if you have not done it before. It will require you to obtain data maps of statistical areas and construct queries to find the location of your coordinates within these maps. It will also require extraction and matching of census/survey data for those statistical areas. (Some resources to get you started can be found here, here and here.) However, if you can do this, it will let you convert your coordinate variables to useful data on the characteristics of the corresponding statistical area. This could potentially give you a number of useful explanatory variables.

Answer 2

While Ert's and Ben's answers are excellent, they rely on the assumption that you understand how to perform statistical modelling on time series, which is not a trivial topic. Entire books are written on this and this simple answer is only an quick introduction using linear regression as an example.

---

Time series linear regression

Assumptions

As with linear regression of cross-sectional data, time series regression requires a set of assumptions to be met in order to perform statistical inference. The strongest set of assumptions are the Gauss Markov conditions, which are often impractical with real data. A weaker set of assumptions are the asymptotic Least Squares.

Given a model

$$ Y_t = \alpha + \beta_1 X_{1t} + \beta_2 X_{2t} + ... + \epsilon_t$$

We require the following:

1. Linear model: $Y_t = \alpha + \beta_1X_{1t} + \beta_2X_{2t} + \epsilon_t$
2. Stationarity in mean, variance and covariance
3. Weak dependence, i.e. correlation tends to zero $ Corr(X_t , X{t + h}) \rightarrow 0 \ \ \text{as} \ \ h \rightarrow \infty$
4. Weak exogeneity $E[\epsilon_t | X_{it}] = 0$ - note that this is less restrictive than the strict exogeneity assumption, as it does not depend on all times, but only on the particular time $t$
5. No perfect colinearity - as usual for Gauss Markov conditions
6. $Var(\epsilon_t | X_{it}) = \sigma^2$ - this is less restrictive than Gauss Markov as it is only for the particular $t$
7. $Cov(\epsilon_t, \epsilon_s | X_t, X_s) = 0$ - less restrictive than Gauss Markov as only depends on time $t$ and $s$.

If assumptions 1 - 5 are satisfied then the parameter $\beta_{LS}$ are consistent. Additional assumptions 6,7 allow to perform inference using the CLT etc...

If all these assumptions are satisfied then you can perform a straightforward linear regression on the model, and use a t-test to test for the significance of a single variable, or an F-test for the significance of the whole model. Have a look here for a recap of the maths and a Python implementation

When assumptions are not met

The reason entire books are written on this topic is that dealing with violations of these assumptions can be difficult, and often requires some subjective decision makings, various statistical tests, pre-processing steps etc...

An example

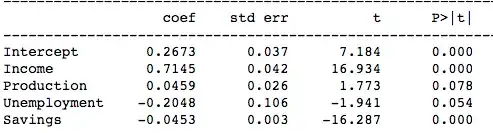
Consider fitting a linear model on US consumer expenditure % change levels based on % change in income, production, savings and unemployment.

A few checks on the data show that the above assumptions are mostly met. Fitting a linear regression model and performing t-tests on the significance of the variables gives

The fitted model isn't too bad

Source

• https://otexts.org/fpp2/least-squares.html

Answer 3

Considering you have a number of features and you are looking to understand how the features affect the price, one straightforward way of doing this would be a regression method, with the following parameters...

• Latitude (continuous)
• Longitude (continuous)
• City (factor, encoded)
• State (factor, encoded)
• Number of bedrooms (factor)
• Number of bathrooms (factor)
• Year built (factor)
• Original price/price during year of building (continuous)

These data would be organized (after being factorized, probably in R or Python) in a matrix, $X$ such that the rows correspond to observations (individual homes) and the columns correspond to the factors above. The $y$ vector would be made of the current home value.

You may consider leaving out the city variables and focusing on longitude and latitude as a proxy for location. State could be enlightening, as taxes and home prices across state lines can vary dramatically.

You could run a regression-based method (maybe not standard linear regression, but a derivative thereof), the coefficient values of which would tell you how each factor relates to the price movement.