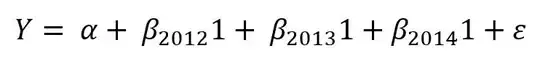How to test the equality of coefficients in a quantile regression?

Question

I run this model on the 95th percentile (Stata 14)

β(2012) 1 : 1 is a dummy variable when Y is observed in 2012 
β(2013) 1 : 1 is a dummy variable when Y is observed in 2013 
β(2014) 1 : 1 is a dummy variable when Y is observed in 2014

I want to test the equality of β(2012) and β(2013). Does quantile regression assumes the normality of the distribution? In other words, can I simply run a T-test for this coefficients equality test?

[A similar question was asked here.](https://stats.stackexchange.com/q/124796/1352) A potential reference was given in a [comment](https://stats.stackexchange.com/questions/124796/testing-for-statistical-differences-of-quantile-regression-line-slopes#comment237867_124796), but since there is no upvoted or accepted answer, we can't close this question as a duplicate of that one. — Stephan Kolassa, Aug 08 '18 at 21:04

dimitriy · Accepted Answer · 2018-08-09T21:18:11.203

You can just do a Wald test on the coefficients directly or via margins:

. sysuse auto
(1978 Automobile Data)

. qreg price i.rep78, quantile(0.5) nolog

Median regression                                   Number of obs =         69
  Raw sum of deviations    65163 (about 5079)
  Min sum of deviations    63340                    Pseudo R2     =     0.0280

------------------------------------------------------------------------------
       price |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
       rep78 |
          2  |        170   1745.715     0.10   0.923    -3317.467    3657.467
          3  |       -185   1612.622    -0.11   0.909    -3406.584    3036.584
          4  |        864   1645.876     0.52   0.601    -2424.015    4152.015
          5  |        463   1697.437     0.27   0.786     -2928.02     3854.02
             |
       _cons |       4934   1561.415     3.16   0.002     1814.715    8053.285
------------------------------------------------------------------------------

. test _b[5.rep78] = _b[3.rep78] 

 ( 1)  - 3.rep78 + 5.rep78 = 0

       F(  1,    64) =    0.69
            Prob > F =    0.4082

. margins rep78, pwcompare(pveffects)
Warning: cannot perform check for estimable functions.

Pairwise comparisons of adjusted predictions
Model VCE    : IID

Expression   : Linear prediction, predict()

-----------------------------------------------------
             |            Delta-method    Unadjusted
             |   Contrast   Std. Err.      z    P>|z|
-------------+---------------------------------------
       rep78 |
     2 vs 1  |        170   1745.715     0.10   0.922
     3 vs 1  |       -185   1612.622    -0.11   0.909
     4 vs 1  |        864   1645.876     0.52   0.600
     5 vs 1  |        463   1697.437     0.27   0.785
     3 vs 2  |       -355   878.6573    -0.40   0.686
     4 vs 2  |        694   938.2936     0.74   0.460
     5 vs 2  |        293   1026.051     0.29   0.775
     4 vs 3  |       1049   658.3504     1.59   0.111
     5 vs 3  |        648   778.3381     0.83   0.405
     5 vs 4  |       -401   845.0837    -0.47   0.635
-----------------------------------------------------

Edit:

You can do a one-sided test like this:

qreg price i.rep78, quantile(0.5) nolog
local sign_diff = sign(_b[5.rep78] - _b[3.rep78])
testnl _b[5.rep78] - _b[3.rep78] = 0
display "H_0: _b[5.rep78] >= _b[3.rep78] p-value = " normal(`sign_diff'*sqrt(r(chi2)))

or perhaps like this:

qreg price i.rep78, quantile(0.5) nolog
local sign_diff = sign(_b[5.rep78] -_b[3.rep78])
test _b[5.rep78] = _b[3.rep78] 
display "H_0: _b[5.rep78] >= _b[3.rep78] p-value = " 1-ttail(r(df_r),`sign_diff'*sqrt(r(F)))

If I want to test : `test _b[5.rep78] >= _b[3.rep78]`, how does this change the critical value of the Wald Test? — user399035, Aug 09 '18 at 00:46
There was a thread about this on SO yesterday: https://stackoverflow.com/q/51734678/1187671 — dimitriy, Aug 09 '18 at 00:48
This is what I am wondering though, since the post (link) is a test related to a scalar `test _b[_cons] = 10`. Is it the exact same process when we compare 2 coefficients `test _b[5.rep78] >= _b[3.rep78]` ? — user399035, Aug 09 '18 at 00:58
e.g. `local sign_rep = sign(_b[5.rep78] - _b[3.rep78])` `display "H_0: 5.rep coef >= 3. rep coef. p-value=" ttail(r(df_r),`sign_rep'**sqrt(r(F))) — user399035, Aug 09 '18 at 01:12
It's testing a less than or equal to hypothesis, which uses an equality hypothesis test as an ingredient. — dimitriy, Aug 09 '18 at 01:12

How to test the equality of coefficients in a quantile regression?

1 Answers1