14

I was recently looking for ways to resample time series, in ways that

  1. Approximately preserve the auto-correlation of long memory processes.
  2. Preserve the domain of the observations (for instance a resampled times series of integers is still a times series of integers).
  3. May affect some scales only, if required.

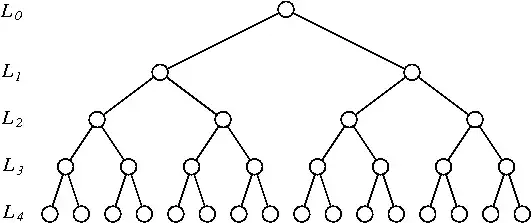
I came up with the following permutation scheme for a time series of length $2^N$:

  • Bin the time series by pairs of consecutive observations (there are $2^{N-1}$ such bins). Flip each of them (i.e. index from 1:2 to 2:1) independently with probability $1/2$.
  • Bin the obtained time series by consecutive $4$ observations (thre are $2^{N-2}$ such bins). Reverse each of them (i.e. index from 1:2:3:4 to 4:3:2:1) independelty with probability $1/2$.
  • Repeat the procedure with bins of size $8$, $16$, ..., $2^{N-1}$ always reversing the bins with probability $1/2$.

This design was purely empirical and I am looking for work that would have already been published on this kind of permutation. I am also open to suggestions for other permutations or resampling schemes.

amoeba
  • 93,463
  • 28
  • 275
  • 317
gui11aume
  • 13,383
  • 2
  • 44
  • 89
  • Your procedure is interesting but as you describe it, it appears to me that if $2^k$ is the max block size, you basically partition your data into $2^{(N-k)}$ consecutive blocks and then within each block permute pairs, each instance being equal-probable. – muratoa Sep 11 '12 at 11:40
  • Instead of pairs you could define $k_{\text{min}}$ and $k_{\text{max}}$. This way you ensure at least $2^{k_{\text{min}}}$ points are preserved and can move a distance at most $2^{k_{\text{max}}}$. – muratoa Sep 11 '12 at 11:43
  • @muratoa thanks for feedback. I am not sure I follow. If $2^k$ is the max block size the scheme is not like permuting pairs within blocks. For instance, for $k=2$, you can obtain the order `4:3:2:1` with probability 1/8, which is not a pair permutation. As for $k_{\min}$ and $k_{\max}$, this is what I refer to in point 3. This is the way to shuffle scales from $k_{\min}$ and $k_{\max}$. – gui11aume Sep 11 '12 at 15:10
  • you're right I didn't read your first bullet correctly, I thought the min size was 2. – muratoa Sep 11 '12 at 19:59
  • Google "amplitude adjusted surrogate data" created by James Theiler and/or have a look at [Resampling Methods for Dependent Data](http://books.google.es/books/about/Resampling_Methods_for_Dependent_Data.html?id=e4f8sqm439UC&redir_esc=y) by Lahiri. – PeterR Sep 11 '12 at 16:34
  • @PeterR, -1 "google blah" answers are useless. If you have to, leave it as a comment, otherwise, provide some actual detail. – naught101 Nov 07 '12 at 23:53

1 Answers1

14

If you include the last bin of size $2^N$, the random permutation is uniformly chosen from the iterated wreath product of groups of order $2$, denoted $C_2 \wr C_2 \wr ... \wr C_2$. (If you leave out the last possible reversal, then you get a uniform sample from an index $2$ subgroup, the product of two iterated wreath products with $N-1$ factors.) This is also the Sylow $2$-subgroup of the symmetric group on $2^N$ elements (a largest subgroup of order a power of $2$ -- all such subgroups are conjugate). It is also the group of symmetries of a perfect binary tree with $2^N$ leaves all at level $N$ (counting the root as level $0$).

enter image description here

A lot of work has been done on groups like this on the mathematical side, but much of it may be irrelevant to you. I took the above image from a recent MO question on the maximal subgroups of the iterated wreath product.

Community
  • 1
Douglas Zare
  • 10,278
  • 2
  • 38
  • 46
  • Awesome (+1)!! Thanks for the reference to the wreath product and the Sylov 2-subgroup. Forgetting the last (top) reversion was a mistake, in fact it is included in the scheme. – gui11aume Sep 11 '12 at 12:52