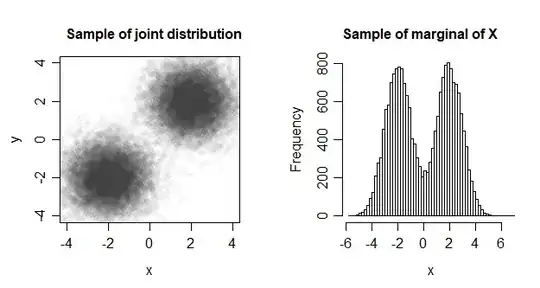
I just would like to understand some information about the joint normality and the margins. I read that the normal joint distribution almost always implies that the univariate margins are all normal.
My question is:
1- Is this apply for Gaussian mixture models? For example, in the Gaussian mixture model, each mixture component follows a Gaussian distribution. Hence, does it imply that each margin will be a Gaussian distribution as well? "I understand that mixture components are used to describe the dependency structures, and they are the joint distribution. is that correct?
2- I read this from one answer to a question in this site here. "So yes, the assumption of joint normality is a sufficient condition for all marginal distributions to be normal, irrespective of the dependence structure. Hence, the theory of Copulas does not affect this result in any way."
However, I really do not understand this: irrespective of the dependence structure. As I understand if the joint distribution in normal then the dependence structure is normal.
Could someone help me with my questions, please?