2

I have come across a problem where I can reasonably assume that the numerator is a uniform distribution of the type U[-a,a], i.e., centered on zero, and the denominator is N[0,b]. This seems to be Cauchy, or at least that is the best answer from simulations and search of best fitting distribution types. Similarly, if I use $\dfrac{N[0,b]}{U[-a,a]}$ rather than $\dfrac{U[-a,a]}{N[0,b]}$, it still seems to be Cauchy. If I use $\dfrac{U[-a,a]}{U[-b,b]}$, it is close to being Cauchy, and as we well know $\dfrac{N[0,a]}{N[0,b]}$ is Cauchy.

Any insights as to what is going on? BTW, there was a superficially similar question, which does not seem to use zero centered uniform distributions, but seems irrelevant to my current problem.

Carl
  • 11,532
  • 7
  • 45
  • 102
  • 6
    Note that you can pull a scale factor out in each case and just look at ratios involving a standard uniform and a standard normal (though with two uniforms you need to put the sign of one of them back in). None of the things you mentioned before the last one is Cauchy. Centered uniform on centered normal is a scaled [*slash*](https://en.wikipedia.org/wiki/Slash_distribution), which was used by Tukey in some robustness studies. The ratio of uniforms is often used in random number generation algorithms, - because of its flat top, it's also called a "table mountain" distribution. – Glen_b Jul 30 '18 at 03:02
  • 1
    They will all be symmetric and will all have fat tails but they differ in their behavior near 0. At the linked post, the case where a=0 and $\mu=0$ is one of the cases you ask about and its density is plotted in two of the answers (both $b$ and $\sigma$ impact the scale but the shape is the same) – Glen_b Jul 30 '18 at 03:39
  • 2
    This is *exactly* the same as the question you reference. The answer there points out that "Different results will be obtained if say parameter a<0, but the procedure is exactly the same." Indeed, you can represent a $U[-a,a]$ variable as an equally weighted mixture of a $U[0,a]$ variable and the negative of a $U[0,a]$ variable and simply apply the answer given there to both components of the mixture. That explains why the graphs in this thread and that one look so remarkably similar: they're essentially the same. – whuber Jul 30 '18 at 14:33
  • @whuber The accepted answer here helped me. The other post did not. – Carl Jul 30 '18 at 15:38
  • 1
    My only hope is that, having had the connection pointed out explicitly, you will appreciate how the other post does help. – whuber Jul 30 '18 at 16:12
  • @whuber Your stats problem solving abilities are still $\sim$10 times what mine are, no slight intended. Maybe it will help to review this when I learn more. – Carl Jul 30 '18 at 18:15

2 Answers2

7

For two independent "benignly" distributed random variables $X$ and $Y$, the ratio $Z = X/Y$ has the pdf $$p_Z(z) = z^{-2} \int_{-\infty}^\infty |x|\, p_X(x)\, p_Y(x/z)\, dx \sim z^{-2}\, p_Y(0)\, \langle|X|\rangle, \quad |z| \to \infty.$$ This indicates why the tails of the ratio are Cauchy-like given that the denominator $Y$ has a smooth finite pdf at zero.

nanoman
  • 481
  • 3
  • 6
  • 1
    +1. For more general analyses of ratio distributions, please see https://stats.stackexchange.com/questions/299722. – whuber Jul 30 '18 at 14:29
2

This gives two answers but not the algebraic steps to prove it. Using Mathematica one can find the density for the ratio $N/U$:

d = TransformedDistribution[z/u, {z \[Distributed] NormalDistribution[0, b], 
    u \[Distributed] UniformDistribution[{-a, a}]}];
PDF[d, r]

$$\frac{b \left(1-e^{-\frac{a^2 r^2}{2 b^2}}\right)}{\sqrt{2 \pi } a r^2}$$

For the density at $r=0$, one could take the limit of the above function as $r \rightarrow 0$:

Limit[PDF[d, r], r -> 0]

$$\frac{a}{2 \sqrt{2 \pi } b}$$

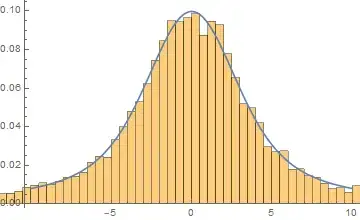
As a check one could perform some simulations:

n = 10000;
zz = RandomVariate[NormalDistribution[0, 1], n];
uu = RandomVariate[UniformDistribution[{-1/2, 1/2}], n];
rr = zz/uu;]
density = PDF[d /. {a -> 1/2, b -> 1}, r];
Show[Histogram[rr, {0.5}, "PDF", PlotRange -> {{-10, 10}, All}],
 Plot[density, {r, -10, 10}]]

Histogram and density function

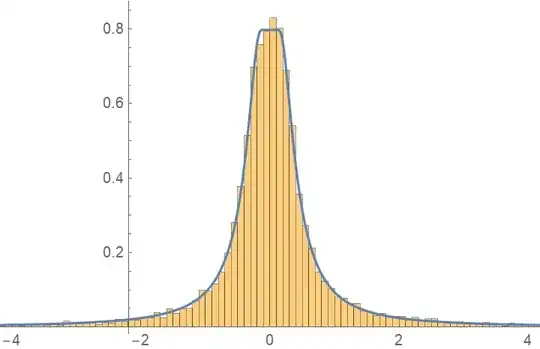
For the ratio $U/N$ one can find the density as follows:

d = TransformedDistribution[u/z, {z \[Distributed] NormalDistribution[0, b], 
    u \[Distributed] UniformDistribution[{-a, a}]}];
PDF[d, r]

$$\begin{array}{cc} \{ & \begin{array}{cc} \frac{b}{\sqrt{2 \pi } a} & r=0 \\ \frac{b \left(1-e^{-\frac{a^2}{2 b^2 r^2}}\right)}{\sqrt{2 \pi } a} & r \neq 0 \\ \end{array} \\ \end{array}$$

Here, too, simulations help:

n = 10000;
zz = RandomVariate[NormalDistribution[0, 1], n];
uu = RandomVariate[UniformDistribution[{-1/2, 1/2}], n];
rr = uu/zz;
density = PDF[d, r] /. {a -> 1/2, b -> 1};
Show[Histogram[rr, {0.1}, "PDF"],
 Plot[density, {r, -5, 5}, PlotRange -> {{-4, 4}, All}], 
 PlotRange -> {{-4, 4}, All}]

Density for U over N

JimB
  • 2,043
  • 8
  • 14