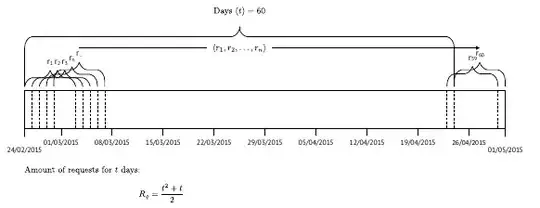
The following example is from chapter 2.12 of Deep Learning, by Goodfellow, Bengio, and Courville:
I don't understand what is meant by the very last part: "Many solutions are possible, because we can increase the scale of $\mathbf{D}_{:, i}$ if we decrease $c^i$ proportionally for all points."
I would appreciate it if people could please take the time to clarify this