What is the probability that $X

Question

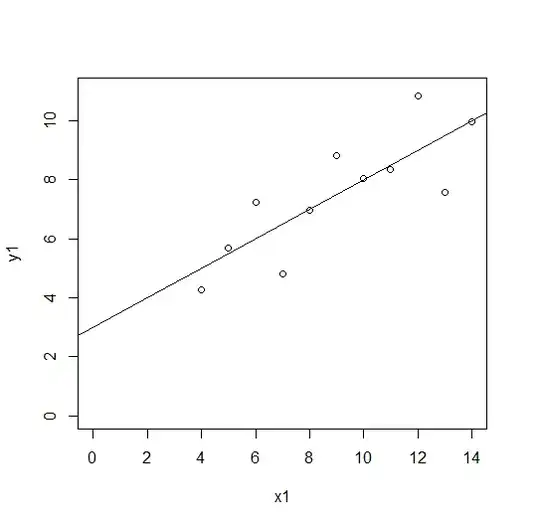
Suppose $X$ and $Y$ are bivariate normal with mean $\mu=(\mu_1,\mu_2)$ and covariance $\Sigma = \begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{12} & \sigma_{22} \\ \end{bmatrix}$. What is the probability $\Pr\left(X<Y|\min\left(X,Y\right)\right)$?

Answer 1

Using the slightly more explicit notation $P(X<Y|\min(X, Y)=m)$, where $m$ is a real number, not a random variable. The set on which $\min(X,Y) = m$ is an L shaped path with two half-open segments: one going straight up from the point $(m,m)$ and another going straight to the right from this same point. It's clear that on the vertical leg, $x<y$ and on the horizontal leg $x>y$.

Given this geometric intuition its easy to rewrite the problem in an equivalent form, where in the numerator we have only the vertical leg where $x<y$ and in the denominator we have the sum of the two legs.

$P(X<Y|\min(X, Y)) = \frac{ \displaystyle P(m<Y|X=m) }{ \displaystyle P(m<Y|X=m) + P(m<X|Y=m) } \tag{1}$

So now we need to calculate two expressions of the form $P(m<X|Y=m)$. Such conditional probabilities of the bivariate normal distribution always have a normal distribution $\mathcal{N}\left(\mu_{X|Y=m}, s^2_{X|Y=m}\right)$ with parameters:

$\mu_{X|Y=m} = \mu_1+\frac{\displaystyle \sigma_{12}}{\displaystyle \sigma_{22}}({m}-\mu_2) \tag{2}$

$s^2_{X|Y=m} = \sigma_{11}-\frac{\displaystyle \sigma_{12}^2}{\displaystyle \sigma_{22}} \tag{3} $

Note that in the original problem definition, $\sigma_{ij}$ referred to elements of the covariance matrix, contrary to the more common convention of using $\sigma$ for standard deviation. Below, we will find it more convenient to use $s^2$ for the variance and $s$ for the standard deviation of the conditional probability distribution.

Knowing these two parameters, we can calculate the probability than $m<X$ from the cumulative distribution function.

$P(m<X|Y=m) = \Phi \left(\frac{\displaystyle \mu_{X;Y=m} -m}{\displaystyle s_{X;Y=m}} \right) \tag{4}$

mutatis mutandis, we have a similar expression for $P(Y>m|X=m)$. Let

$ z_{X|Y=m} = \frac{\displaystyle \mu_{X;Y=m} - m}{\displaystyle s_{X;Y=m}} \tag{5} $

and

$ z_{Y|X=m} = \frac{\displaystyle \mu_{Y;X=m} -m}{\displaystyle s_{Y;X=m}} \tag{6} $

Then we can write the complete solution compactly in terms of these two $z$ scores:

$ P(X<Y|\min(X, Y)=m) = 1 - \frac{ \displaystyle \Phi(z_{X|Y=m}) }{ \displaystyle \Phi(z_{X|Y=m})+\Phi(z_{Y|X=m}) } \tag{7}$

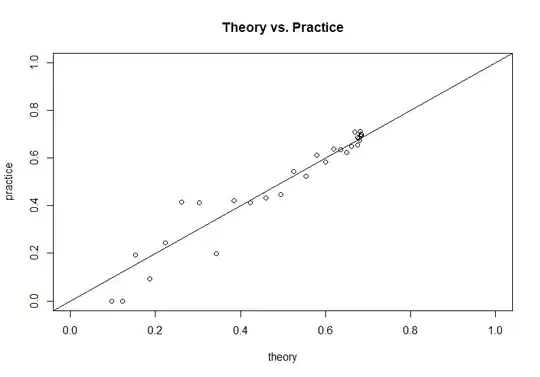
Based on simulation code provided by the question author, we can compare this theoretical result to the simulated results:

Answer 2

The question can be rewritten using a modified version of Bayes theorem (and an abuse of notion for $Pr$)

\begin{align} Pr(X<Y|min(X,Y) = m) &= \frac{Pr(min(X,Y)=m|X<Y)Pr(X<Y)}{Pr(min(X,Y)=m|X<Y)Pr(X<Y)+Pr(min(X,Y)=m|X\geq Y)Pr(X\geq Y)}\\ &= \frac{Pr(X<Y,min(X,Y)=m)}{Pr(X<Y,min(X,Y)=m)+Pr(X\geq Y,min(X,Y)=m)}. \end{align}

Define $f_{X,Y}$ to be the bivariate PDF of $X$ and $Y$, $\phi(x) = \frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}x^2)$ and $\Phi(x) = \int_{-\infty}^x\phi(t)dt$. Then

\begin{align} Pr(X<Y,min(X,Y)=m) &=Pr(X=m,Y>m) \\ &= \int_m^\infty f_{X,Y}(m,t)dt \end{align}

and

\begin{align} Pr(X\geq Y,min(X,Y)=m) &=Pr(X\geq m,Y=m) \\ &= \int_m^\infty f_{X,Y}(t,m)dt \end{align}

Using normality and the definition of conditional probability the integrands can be rewritten as

$$f_{X,Y}(m,t) = f_{Y|X}(t)f_X(m) = \frac{1}{\sqrt{\sigma_{Y|X}}}\phi\left(\frac{t-\mu_{Y|X}}{\sqrt{\sigma_{Y|X}}}\right)\frac{1}{\sqrt{\sigma_{11}}}\phi\left(\frac{m-\mu_1}{\sqrt{\sigma_{11}}}\right)$$

and

$$f_{X,Y}(t,m) = f_{X|Y}(t)f_Y(m) = \frac{1}{\sqrt{\sigma_{X|Y}}}\phi\left(\frac{t-\mu_{X|Y}}{\sqrt{\sigma_{X|Y}}}\right)\frac{1}{\sqrt{\sigma_{22}}}\phi\left(\frac{m-\mu_2}{\sqrt{\sigma_{22}}}\right).$$

Where $$\mu_{X|Y} = \mu_1 + \frac{\sigma_{12}}{\sigma_{22}}(m-\mu_2),$$

$$\mu_{Y|X} = \mu_2 + \frac{\sigma_{12}}{\sigma_{11}}(m-\mu_1),$$

$$\sigma_{X|Y} = \left(1-\frac{\sigma_{12}^2}{\sigma_{11}\sigma_{22}}\right)\sigma_{11}$$

and

$$\sigma_{Y|X} = \left(1-\frac{\sigma_{12}^2}{\sigma_{11}\sigma_{22}}\right)\sigma_{22}.$$

Thus

\begin{equation} Pr(X<Y|min(X,Y) = m) = \frac{\left(1-\Phi\left(\frac{m-\mu_{Y|X}}{\sqrt{\sigma_{Y|X}}}\right)\right)\frac{1}{\sqrt{\sigma_{11}}}\phi\left(\frac{m-\mu_1}{\sqrt{\sigma_{11}}}\right)}{\left(1-\Phi\left(\frac{m-\mu_{Y|X}}{\sqrt{\sigma_{Y|X}}}\right)\right)\frac{1}{\sqrt{\sigma_{11}}}\phi\left(\frac{m-\mu_1}{\sqrt{\sigma_{11}}}\right)+\left(1-\Phi\left(\frac{m-\mu_{X|Y}}{\sqrt{\sigma_{X|Y}}}\right)\right)\frac{1}{\sqrt{\sigma_{22}}}\phi\left(\frac{m-\mu_2}{\sqrt{\sigma_{22}}}\right)}. \end{equation}

This final form is very similar to the result @olooney arrived at. The difference is his probabilities are not weighted by the normal densities.

An R script for numerical verification can be found here