Define the (differential) entropy for density $f$ as
$$ H(f) :=-\int_{0}^{1} f(x) \log_{2}(f(x)) dx \, .$$
I am trying to find a Lebesgue measurable $f$ defined on $[0,1]$ such that $f\geq 0, \int_{0}^{1} f(x) dx = 1$ and $H(f)= -\infty $. I am not sure if this is possible? (The $f$ has to be in $L_{1}([0,1])$ and so the measure induced by $f$ must be absolutely continuous with respect to Lebesgue measure. So, a Dirac delta won't work.)
Yes, there are densities with negatively infinite entropy.
To construct one, find a family of densities with arbitrarily negative entropy. (Clearly this requires the density functions to have arbitrarily large values and therefore there are points where they become "singular.") By shifting and scaling them into disjoint intervals within $[0,1],$ if we are careful we can produce a density whose entropy is close to the average of the entropies of its pieces. Since the average of a divergent sequence diverges, this can produce a function with negatively infinite entropy provided we make sure to push the closure of singularities into a measure-zero subset. The following account gives an explicit construction.
To discuss entropy in a compact way, define the function $h:\mathbb{R}\to\mathbb{R}$ as
$$h(t) = -t\log(|t|) = -t \log(t^2)/2.$$
The second formula immediately shows $h$ is continuous, and differentiable everywhere except at $0.$ It determines the entropy of any density $f$ as
$$H[f] = \int_{\mathbb{R}} h(f(t))\mathrm{d}t.$$
Note that $H[f]$ is defined for any integrable non-negative function $f$ for which $|h(f(t))|$ is integrable, which will include any positive multiples of densities $t\to \lambda f(t).$
For any number $p\lt 1,$ consider the functions $\phi_p:\mathbb{R}\to\mathbb{R}$ whose values are zero everywhere except on the interval $(0,1]$ where they are given by the formula
$$\phi_p(t) = (1-p)t^{-p}.$$
The $\phi(p)$ integrate to unity and they obviously have non-negative (and finite) values, whence they are all density functions. (They are Beta$(1-p,1)$ densities.) Their entropies are
$$H[\phi_p] = -\int_{(0,1]} (1-p)t^{-p} \log((1-p)t^{-p})\mathrm{d}t = -\left(\frac{p}{1-p} + \log(1-p)\right),\tag{1}$$
which can be made arbitrarily negative (but not infinite) by taking $p$ close to $1.$ Notice that the only singularity of $\phi_p$ is at $0.$
Can we do better? We might try to assemble a density out of the $\phi_p$ by shifting them into disjoint intervals, for then the integral involved in the entropy calculation becomes the simple sum of the integrals in each of those intervals. We will need to discover how such alterations to a density change the entropy. For completeness, the following recapitulates the analysis described at How does entropy depend on location and scale?.
In general, when $f$ is any density, let $$f_{\lambda, \mu,\sigma}(t) = \lambda f\left(\frac{t-\mu}{\sigma}\right)$$ be a scaled version (with $\sigma$ and $\lambda$ positive) and change variables to $x = (t-\mu)/\sigma$ to find
$$\int f_{\lambda,\mu,\sigma}(t)\mathrm{d}t = \lambda\sigma \int \lambda f(x)\sigma \mathrm{d}x = \lambda \sigma\tag{2}$$
and
$$\eqalign{ H[f_{\lambda, \mu,\sigma}] &= -\int \lambda f\left(\frac{t-\mu}{\sigma}\right)\log \left(\lambda f\left(\frac{t-\mu}{\sigma}\right)\right)\mathrm{d}t \\ &= -\lambda\sigma\int f\left(x\right)\log \left(\lambda f\left(x\right)\right)\mathrm{d}x \\ &= -\lambda\sigma\left(\int f(x)\log(f(x))\mathrm{d}x + \log(\lambda)\int f(x)\mathrm{d}x\right) \\ &= \lambda \sigma(H[f] - \log(\lambda)). \tag{3} }$$
Let's return to the problem of building a density $f$ out of non-overlapping pieces by shifting and scaling various $\phi_p.$ One way is for each $n=1, 2, 3, \ldots,$ shift and scale $$f^{(n)} = \phi_{1-1/n}$$ into the interval $(1/(n+1), 1/n].$ This is done by setting $\mu_n=1/(n+1)$ and $\sigma_n = 1/(n(n+1))$ above. Let $(\lambda_n)$ be a sequence of positive weights and with them form
$$f(t) = \sum_{n=1}^\infty f^{(n)}_{\lambda_n, \mu_n, \sigma_n}(t) = \sum_{n=1}^\infty \lambda_n\phi_{1-1/n}\left(n(n+1)t - n\right).\tag{*}$$
Result $(2)$ above implies that for $f$ to be a density we must have
$$1=\int f(t)\mathrm{d}t = \sum_{n=1}^\infty \lambda_n \sigma_n = \sum_{n=1}^\infty \frac{\lambda_n}{n(n+1)}$$
and $(3)$ along with $p=1-1/n$ in formula $(1)$ yields
$$\eqalign{ H[f] &= \sum_{n=1}^\infty \frac{\lambda_n}{n(n+1)}(H[\phi_{1-1/n}] - \log(\lambda_n)) \\ &= \sum_{n=1}^\infty \frac{\lambda_n}{n(n+1)}(\log(n) - n + 1 - \log(\lambda_n)). \tag{4} }$$
A simple solution is to take $\lambda_n=1$ for all $n.$
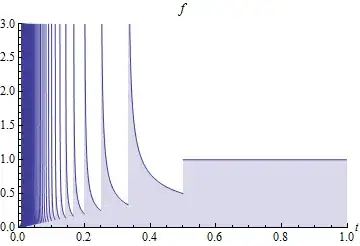
The choice of $\lambda_n$ scales the infinite spikes in this figure so that the total area beneath them is unity. As they move to the left, though, they become "heavier" by making the power $p$ closer to $1.$
This makes $f$ a density and $(4)$ becomes
$$H[f] = \sum_{n=1}^\infty \frac{1}{n(n+1)}(\log(n) - n + 1 - \log(1)) = -\sum_{n=1}^\infty \frac{1 - (\log(n)+1)/n}{n+1}.$$
Since for all positive numbers $\log(n)/n \lt 1/2$, we may take $1/n + 1/2$ to be a lower bound for values $(1+\log(n))/n,$ producing
$$H[f] \lt-\sum_{n=1}^\infty \frac{1 - (1/n+1/2)}{n+1} \lt \sum_{n=1}^\infty \frac{1}{n(n+1)} -\frac{1}{2}\sum_{n=1}^\infty \frac{1}{n+1} = 1-\frac{1}{2}\sum_{n=1}^\infty \frac{1}{n+1},$$
which diverges to $-\infty.$
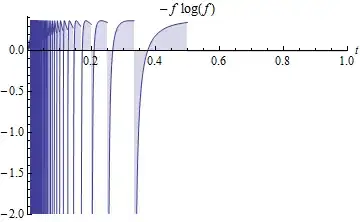
The entropy of $f$ is the (signed) area between this graph of $h\circ f$ and the t-axis. The spikes at the left contribute an infinitely negative area.
Finally, $f$ is defined and has finite values everywhere on $(0,1].$ Although it has infinitely many singularities, they are countable in number, isolated, and condense only at $0,$ making it clear that $f$ is absolutely continuous with respect to Lebesgue measure on $(0,1].$
For the record, $(*)$ works out to
$$f(t) = \frac{1}{n}\left(n(n+1)t - n\right)^{1/n-1}$$ where $n$ is the greatest integer less than or equal to $1/t$ and $0\lt t\le 1.$ We have shown that $f$ is a density and $H[f] =-\infty.$
I actually came across to this problem from a different angle. I was trying to understand why the mutual information of multivariate normal distribution goes to $\infty$ as the correlation goes to 1. See here
So to your question, sorry I don't know the answer, but if we loose the condition $H(f)=-\infty$ to any arbitrary negative number and consider multivariate functions, then $f(x)$ can be the joint pdf of enough correlated (correlation close to 1) bivariate normal distribution.
