Coordinate descent with constraints

Question

When performing constrained optimization on a smooth, convex function using coordinate descent, for what types of constraints will the algorithm work ? (i.e. converge or reach an approximate optimum within a tolerance of the constraint)

My understanding is that coordinate descent will work for

• Box constraints: e.g. $x_1 \leq -1$ and $x_2 \leq -1$
• Linear constraints: e.g. $x_2 \leq -x_1 -1$
• Any others ?

In other words, how can we know whether or not coordinate descent can be applied to a contrained optimization problem ?

PS: irrespective of whether this is the right algorithm to use

Answer 1

The bland answer is that to solve constrained optimization problems, you need an algorithm that knows and uses the constraints - simply applying unconstrained optimization algorithms will not work.

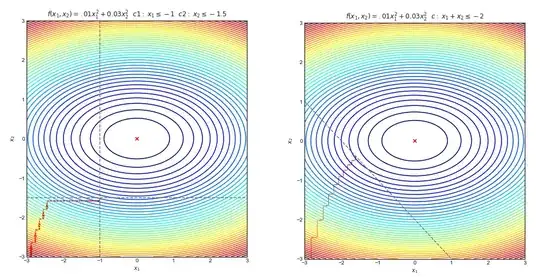
Box constraints

Taking the algorithm you described in your answer, it will ''not work'' for box constraints, depending on the value of the step-size $\alpha$;

Take $f(x) = x$, $x \leq 0.9$, start at $x_0 = 0$ with a step-size $\alpha=1$.

The only step available does not satisfy the constraint.

You can decrease $\alpha$ to make it ''work'', but you can always find a function/starting point for which it does not work; the correct step-size depends on the interaction between the function and the constraints and thus require solving a constrained optimization problem to set it.

If you are able to solve the subproblem of finding the minimum along the dimension you are optimizing while respecting the constraint, i.e. taking steps $$x_i^{k+1} = \arg \min_{x_i \in C} f(x_1^{k}, ..., x_{i-1}^{k}, x_i, x_{i+1}^{k}, ..., x_D^{k}),$$ you can solve box constraints, as in your first reference.

Linear constraints

However, this approach will choke on linear constraints.

Take $f(x,y) = x^2 + y^2$, with $x + y < -1$. The minimum is at $(-0.5,-0.5)$, but if you start at $(-1,0)$ you can not make progress on $x$ (not allowed to be bigger than $-1$) nor $y$ (is at the minimum given $x = -1$).

Your second ref. is able to get around that issue by considering block coordinate updates; changing $k$ coordinates at each iteration makes it possible to get around linear constraints involving less than $k$ variable at a time.

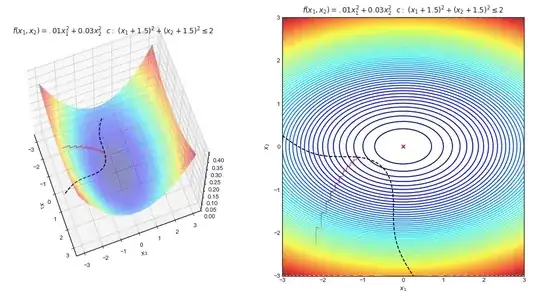
Non-linear constraints

Your non-linear constraint is also non convex; start at $(0,-3)$ and the algorithm would converge to $(0, -2.9...)$, not at the minimum.

What to do

You can either use a constrained optimization algorithm (Frank-Wolfe comes to mind) or re-parametrize your problem so that it incorporates the constraints; if you want to find the minimum of $f(x), x \geq 0$, try to find the minimum of $g(y) = f(y^2), y \in \mathbb{R}$

Answer 2

Perhaps this question is more difficult than I thought, or would be better asked on math.stackexchange.com. But since it arose in the context of SVM I will leave it here.

There are some papers discussing coordinate descent and constrained optimization with the following key words.

• Linear and box constraints and blocks of primal variables here
• Coupled constraints, Compact convex sets and Polyhedra here
• A cryptic MIT paper

While the mathematics are beyond me, I will proceed to show visually and experimentally that for the following toy, convex function, coordinate descent works for box, linear and highly non linear constraints.

Consider the function to be minimized:

$$f(x_1,x_2) = .01x_1^2 + 0.03x_2^2$$ $$\nabla f = [2 \times 0.01 x_1, 2 \times .03 x_2]$$

Since the gradient has only terms in $x_1$ and $x_2$ respectively, we can evaluate it at each step $k$ holding the other variable constant. Checking the constraint at each step allows to

• Do nothing if $x_i^{(k+1)}$ has a value outside the constraint boundary
• Update $x_i^{(k+1)} = x_i^{(k)} - \alpha \ \nabla_i \ f(x_1, x_2)$ otherwise

---

A few examples

1) Box and 2) linear constraints

• $c1: \ x_1 \leq -1 \ \ c2: \ x_2 \leq -1.5 $
• $c: \ x_1 + x_2 \leq -2$

3) Non linear constraint

• $c: \ (x_1 + 1.5)^3 + (x_2 + 1.5)^3 \leq 2$

Next steps

Perhaps a function which is convex, but whose gradient has cross terms $x_1x_2$ will prove more difficult or even impossible to optimize using CD