Missing steps in Bellman Equation and MDP assumptions

Question

My question is similar to this one. I am trying to fill in the missing steps of the Bellman equation for a Markov Decision Process:

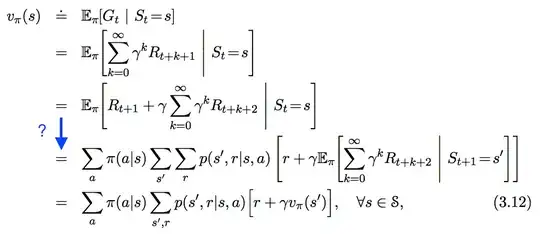I will focus on the first term of the sum $R_{t+1} + \gamma \sum_{k=0}^{\infty}\gamma^kR_{t+k+2}.$ Here's my attempt:

$$ \begin{align} & E_{\pi}[R_{t+1}|S_t=s] \\ &= \sum_{s'} \sum_a E_{\pi}[R_{t+1}|S_t=s, S_{t+1}=s',A_t=a]P(S_{t+1}=s',A_t=a)\\ & =\sum_{s', a, r} rP(R_{t+1}=r|S_t=s, S_{t+1}=s', A_t=a)P(S_{t+1}=s', A_t=a)\\ &= \sum_{s', a, r} r \frac{P(R_{t+1}=r,S_t=s, S_{t+1}=s', A_t=a)}{P(S_t=s, S_{t+1}=s',A_t=a)}P(S_{t+1}=s', A_t=a)\\ &= \sum_{s', a, r} r \frac{P(S_{t+1}=s', R_{t+1}=r|S_t=s, A_t=a)P(S_t=s,A_t=a)}{P(S_t=s, S_{t+1}=s',A_t=a)}P(S_{t+1}=s', A_t=a)\\ &= \sum_{s', a, r} r \frac{p(s',r|s,a)P(A_t=a|S_t=s)P(S_t=s))}{P(S_t=s, S_{t+1}=s',A_t=a)}P(S_{t+1}=s', A_t=a)\\ &= \sum_aP(A_t=a|S_t=s)\sum_{s',r}r p(s',r|s,a) \frac{P(S_t=s)P(S_{t+1}=s', A_t=a)}{P(S_t=s, S_{t+1}=s', A_t=a)} \end{align}$$

Some questions:

Is it true that $P(S_t=s, S_{t+1}=s', A_t=a) = P(S_t=s)P(S_{t+1}=s', A_t=a)$? I am under the impression that the next state depends on both the action taken and the previous state? I.e. are these events independent or not?

If we do have independence, then is my derivation correct? Is there a simpler way to show the result?

I'm also a bit confused about the two underlying distributions here: $p$ and $\pi$. Are they in no way related to each other? Isn't it possible that $p(s',r|s,a) = P(S_{t+1}=s', R_{t+1}=r|S_t=s,A_t=a)$ induces a distribution on $P(A_t=a|S_t=s) = \pi(a|s)$?

Answer 1

To answer your questions in reverse order (shortest answer first) -

$\pi(a|s)$ is the policy, also known as the decision rule, whereas $p(s'|s,a)$ is the state transition probability distribution. They are in no way related to each other, except insofar as the objective of analyzing an MDP is often to find the best policy, and which policy is best is a function of the transition probability distributions (and rewards.) If your policy is deterministic, then $\pi(a|s) = 1$ for the action that you will choose when in state $s$, $0$ for all other actions, but policies need not be deterministic.

It doesn't seem to me from the question that you want the derivation itself, but some strong hints as to how to go about it, so that's what follows.

When you are at stage $t$, the state $s_t$ is known. Consequently, when deciding what action to take or calculating the probability of transitioning to the next state, there is no need to invoke a probability distribution $P(S_t = s)$. That is why, in the original text, $s$ is always on the right of the "$|$", and only $s'$ - the state after the next transition - is on the left of the "$|$". Note that what you are trying to derive is an expression for $v(s)$; you could hardly do so if $s$ isn't fixed at the time of calculation!

When you moved from the third line of your series of equalities to the fourth, you changed $s$ from being something that the rest of the expressions are conditioned on to a random variable, which was a mistake. However, you had already made a mistake in your second line, as you are summing over $a$, but have put taking the expectation with respect to $\pi$ - which is, essentially, summing over $a$ while multiplying by $\pi(a|s)$ - inside the summation. You have thereby created a nested sum of the form $\sum_a \sum_a \text{stuff }* \pi(a|s)$, which obviously won't work.

A better approach would be to mimic the structure of the pasted text. Note that in the third line, $\mathbb{E}_{\pi}$ is outside the square brackets; this enables everything within the square brackets to be calculated conditional upon the action, and, only at the end, do we integrate out the action based on the policy - that's what the term $\sum_a \pi(a|s)$ does. Thus, $R_{t+1}$ is conditional upon both the action $a$ and the state $s$; that is why, when moving to the line immediately after the blue arrow, you have the expression $p(s', r|s,a)$. $s'$ and $a$ are both integrated out by the summation over $s'$ and the summation over $a$ while multiplying by $\pi(a|s)$ respectively, leaving you with something that can be denoted $p_{\pi}(r_{t+1}|s_t)$, the probability of seeing reward $r$ at time $t+1$ given the state at time $t$ ($s_t$) and the policy $\pi$.