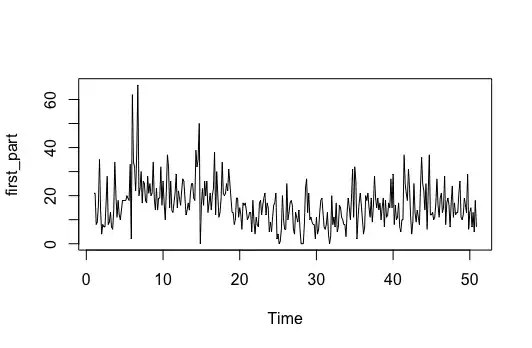
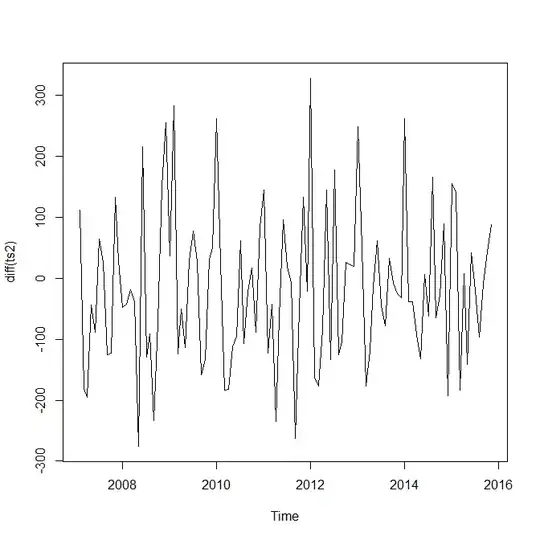
I have a time series, which I would want to model using Sarima + regression. However, I have a binary variable which clearly controls the level of the time series (for the dates when it is set to 1, the time series level is 20%-100% higher). I read this explanation by R. Hyndman:
https://www.otexts.org/fpp/9/1
and it says:
"An important consideration in estimating a regression with ARMA errors is that all variables in the model must first be stationary. So we first have to check that ytyt and all the predictors (x1,t,…,xk,t)(x1,t,…,xk,t) appear to be stationary...
So we first difference the non-stationary variables in the model. It is often desirable to maintain the form of the relationship between ytyt and the predictors, and consequently it is common to difference all variables if any of them need differencing.".
This confused me a little (completely). Do we take the difference of binary variables too? If we had a series of predictors 000111000 it will become 000100-100 that does not look like something I would want to regress on at all.
In addition to the above, is it actually possible to simply fit a regression model to the data, compute the errors, and then fit the usual ARIMA to these errors? I think i saw some answer here on modelling with exogenous variables, but cannot find it anymore.
The exogenous variable is set to 1 for periods indicated as peaks in time series in the pic (between 5-6, and 14-15):
This data is as follows (2 columns):
population: 21 21 8 9 16 35 14 4 8 7 7 17 28 8 9 13 7 6 14 34 20 11 18 12 10 14 18 18 18 18 20 19 18 33 2 62 34 32 22 38 66 20 23 30 17 26 25 18 17 28 21 25 20 21 34 19 14 23 14 19 19 32 16 26 17 10 22 37 32 15 26 14 13 17 21 29 15 22 19 16 22 27 26 19 12 14 17 14 21 25 25 19 18 39 32 35 50 0 16 23 16 26 20 26 13 17 21 14 20 23 38 12 30 20 11 13 19 34 21 20 21 25 22 31 25 19 13 13 8 10 19 19 11 15 12 6 17 16 17 14 10 11 13 13 5 18 9 4 11 8 7 17 18 12 16 19 21 12 17 15 5 9 5 11 16 17 21 2 4 0 1 6 20 10 6 6 25 10 13 17 18 16 6 4 13 11 9 14 6 0 0 0 8 23 27 13 21 10 11 9 8 8 2 11 4 6 13 18 19 13 7 6 8 13 4 0 3 20 8 11 7 17 5 7 16 15 11 10 8 8 3 13 19 15 10 19 31 11 32 26 2 11 17 21 16 10 4 7 20 18 21 15 11 19 9 16 28 19 15 19 14 17 10 15 19 7 18 11 12 17 15 27 15 29 8 16 10 11 17 7 5 10 10 37 25 21 18 31 23 11 4 9 25 13 9 14 11 8 24 36 25 22 14 25 6 21 37 12 12 13 10 11 17 27 16 11 19 21 13 15 28 8 17 19 16 7 17 24 11 17 12 13 13 21 26 11 10 12 19 16 13 29 6 13 15 7 13 5 18 7
ad: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0