1

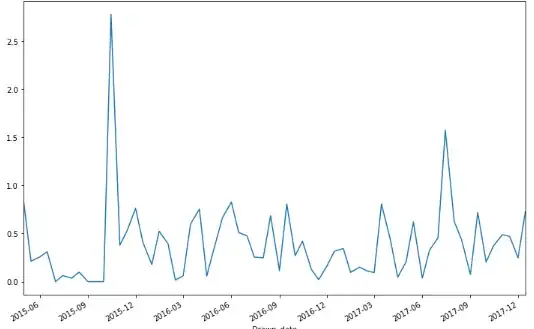
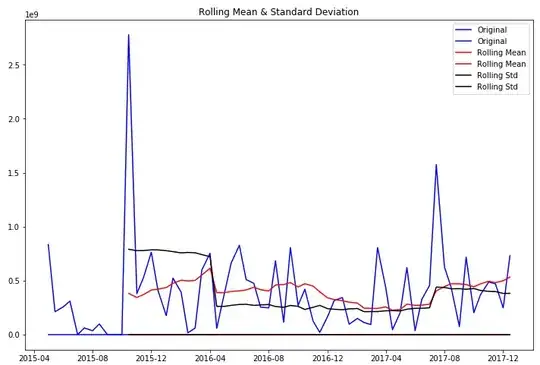
I am working on a bimonthly data where I have customer the customer's sales amount. I tried to plot the original series in python and the plot

import matplotlib.pyplot as plt

Cust_bimonthly_Data['Customer_Sales'].plot(figsize=(12, 8))
plt.title('Cust Bimonthly Daily')
plt.show()

I tried to plot the above time series in Python and it looks like this

enter image description here

enter image description here

In order to remove this big peak in my data which was an outlier I did log(x+1) transformation on my data i.e. increased all the values to 1 and then did a log transformation

Cust_bimonthly_Data['new_Customer_Sales'] = Cust_bimonthly_Data['new_Customer_Sales']+1

taking the log so as to remove the outliers

Cust_bimonthly_Data['log_cust_sales']=np.log(Cust_bimonthly_Data['new_Customer_Sales'])

**the log transformed series looks like this **

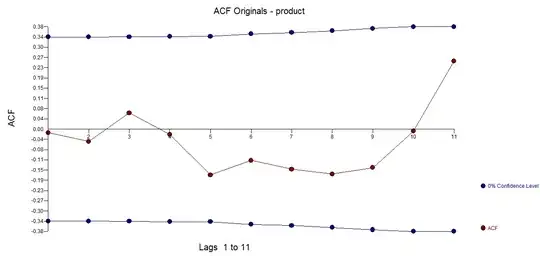
enter image description here

In order to check if my log transformed data is stationary or not I did a ADF test and this is what my results look like

Dickey Fuller test to check if the series transformed series is stationary or not

from statsmodels.tsa.stattools import adfuller
Cust_bimonthly_Data_test= Cust_bimonthly_Data_drop.iloc[:,0].values
result = adfuller(Cust_bimonthly_Data_test)

(-4.8014847417664424,
5.4031369234729222e-05,
0,
63,
{'1%': -3.5386953618719676,
'10%': -2.591896782564878,
'5%': -2.9086446751210775},
150.10425215395222)

question?

Since this test is rejecting the null hypothesis that my series is not stationary , should I still go ahead and perform the decomposition and differencing part. I mean will all those things would still be required since I can see the test tells me that my series is now stationary

Community
  • 1
Swati Kanchan
  • 13
  • 3
  • It appears the customer is buying irregularly but is making up for periods of low purchases by one-time larger purchases. By exploiting this fact (if indeed it is correct), you can produce a model that will be far more insightful and accurate than anything any automatic procedure can do for you. It really wouldn't be appropriate to supply specific advice until you can explain what your objectives in this analysis are. (Only an academic researcher would ultimately be interested in the question of stationarity.) – whuber Jun 23 '18 at 20:37
  • The automatic analysis suggested that the customer is indeed buying irregularly as there is no identifiable pattern i.e. arima structure or memory structure. There is only 1 "large purchase" which suggests a unusual activity which at this point can't be predicted just identified and adjusted for. – IrishStat Jun 23 '18 at 21:03
  • @Irish I am trying to suggest that such large purchases *are* likely predictable: the probability of a large purchase ought to increase after a series of small purchases, at least if the customer's needs are roughly constant over time. However, because it's unlikely any ARIMA-like model will handle such a phenomenon appropriately, there is potentially great value in constructing a model that addresses these circumstances. – whuber Jun 24 '18 at 19:32
  • What AUTOBOX developed was the anthesis of an arima-type model as neither previous values nor previous errors were identified/suggested factors/features of the model. What is suggested is that three events were triggered by unspecified exogenous variables. The two pulses and the shift in mean suggest that one investigate the root exogenous cause . This Exploratory Data Analysis is meant to drive the investigation by implicitely "asking the user" to find out the "whys" . – IrishStat Jun 25 '18 at 09:24

2 Answers2

2

One doesn't take logs or any other power transform to deal with anomalous observations like pulses,level shifts,seasonal pulses or local time trends . See When (and why) should you take the log of a distribution (of numbers)? for when to power transform and see http://docplayer.net/12080848-Outliers-level-shifts-and-variance-changes-in-time-series.html for how to deal with anomalies.

Also the dickey-fuller test requires/assumes that any and all pulses,level shifts,seasonal pulses and local time trends have been incorporated into the model and thus are not present in the current set of residuals.

It looks like you have at least 2 pulses and 2 possible level shifts and possible arima structure. Post your data and I will try and help.

EDITED AFTER RECEIPT OF DATA..

I took your 33 bi-monthly values ( too short to look for seasonal structure ) and used AUTOBOX and obtained the following Actual/Fit and Forecast graph

enter image description here . Two pulses and one level shift ...

enter image description here The stats are here enter image description here and here enter image description here

The acf of the residuals is here enter image description here suggesting randomness.

(1) IN RESPONSE TO OP'S QUESTION:

the acf of the original series does not suggest non-stationarity enter image description here because the level shift obfuscated the variance creating a downwards bias to the acf. Non-stationarity was detected by detecting the presence of a level shift via exploratory data analysy suggesting the need (mandatory) to introduce a level/step shift EXOGENOUS series as the remedy for the non-stationarity .

IrishStat
  • 27,906
  • 5
  • 29
  • 55
0

Perhaps one could assume that data is generated by the linear combination of two processes, one producing seasonality plus perhaps trend and other which incorporates unit impulses to the level of series by certain probability.

As IrishStat mentioned your complete model must be able to handle that.

Of course you could use Autobox which David Reilly has created....

Analyst
  • 2,527
  • 10
  • 11