My project is focused on Crime Prevention Through Environmental Design, AKA CPTED. CPTED is a theory that certain characteristics of the built environment, such as level of maintenance, level of visibility, and personal touches, can help prevent crime.
I want to see if areas (neighborhood blocks) with more CPTED characteristics also have a lower crime count. My hypothesis is that the areas with higher CPTED rating will have a lower crime count, and areas with a lower CPTED rating will have a higher crime count.
The data collection has already been done. For my research, I made observations of houses of 6 neighborhoods, and rated all of the houses based on CPTED characteristics. The rating system is from 0 (worst) to 4 (best). Higher CPTED ratings are meant to be “better,” meaning these houses have a lower risk of being targeted for property crime.
Once all of the houses in each of the 6 neighborhoods were rated and recorded in a spreadsheet, I assigned each house to a neighborhood block, and the blocks were given the combined average CPTED score.
I then obtained data of crime incidents from the local police department and assigned the crime incidents to the blocks, because most crime reports nowadays only have block-level accuracy, instead of giving specific addresses. This is the reason that the individual house lots had to be aggregated into larger neighborhood blocks.
To recap, I have:
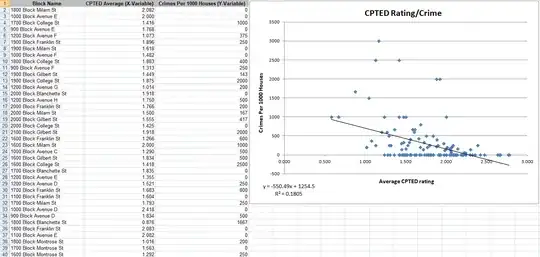
A spreadsheet which has a column for Average CPTED Rating (the X variable), and a column for Crimes Per 1,000 Houses (The Y variable). A screenshot of this spreadsheet is here:
I already ran a regression analysis on this data, and the result shows that as the CPTED rating increases, the crime count decreases. However, this seems to be a somewhat weak inverse relationship, with an R-Squared value of .18. But I now am questioning whether or not a regression analysis is appropriate for this type of study.
Could I perform some sort of non-parametric test? I am still a bit of a novice when it comes to these types of statistics. Are there any non-parametric tests that I could use on this data to determine the relationship between CPTED rating and crime count? I have been encouraged to use a non-parametric test but I am not sure which one, if any, would be appropriate. I have had one statistics “expert” in a forum recommend using the Spearman’s Rho test, and that seemed like a good idea until another “expert” told him that was incorrect.