Regularized parameter overfitting the data (example)

Question

Possible duplicate of

• (Why) do overfitted models tend to have large coefficients?
• How does regularization reduce overfitting?

In the Coursera's machine learning course by Andrew Ng, I came across the following example.

$C = 1/ \lambda$ i.e. the inverse of the actual regularization parameter.

The L2 regularization cost expression is $ R = \Sigma_{i=1}^{n} \theta_i^2 $

For black classifier, we have $h_{\theta}(x) = -3 + x_1\;\; \theta = [-3, 1, 0] \;\; R = 10$

For magenta classifier, we have $h_{\theta}(x) = -1 + x_1 - x_2 \;\; \theta = [-1, 1, -1] \; \; R = 3$

Regularization cost for magenta classifier is low but still it seems to overfit the data and vice-versa for the black classifier. What's going on? L2 regularization tend to make the coefficients close to zero. But how does that helps in reducing overfitting?

The intuition what I think of is that not much weight is given to a particular feature. But isn't it sometimes necessary to focus on one feature (like in the above example $x_1$)?

Answer 1

Regularization cost for magenta classifier is low but still it seems to overfit the data and vice-versa for the black classifier. What's going on? L2 regularization tend to make the coefficients close to zero. But how does that helps in reducing overfitting?

Overfitting isn't about what happens to the training data alone. It's about the comparison of the training data and out-of-sample. If your training loss is low, but your out-of-sample loss is large, you're overfitting. If your training loss is low, and your out-of-sample loss is low, congrats! You have some evidence that your model generalizes well.

So if we apply that definition here, it’s obvious that we can’t say anything about whether the model is over- or under-fit because there’s no comparison to out of sample data.

Regularization can help with overfitting by discouraging the model from estimating too-complex a decision boundary. The diagonal/magenta decision boundary could be "too-complex" (as measured by $L^2$ regularization omitting the intercept) if the X far away from the other Xs and near the Os is not representative of the process overall (i.e. it is a quirk).

The intuition what I think of is that not much weight is given to a particular feature. But isn't it sometimes necessary to focus on one feature (like in the above example x1)?

Preventing "too much weight given to a particular feature" isn't what $L^2$ regularization does, but does sound more like $L^\infty$ regularization (which tends to result in weights that are more evenly distributed). $L^2$ regularization penalizes large coefficients (or encourages coefficients to be nearer to zero).

The distinction I'm making is subtle, but the point is that in $L^2$ regularization, a model can "put its eggs all in one basket" and have a small number of large coefficients and many near-zero coefficients. This is desirable when there are only a few highly relevant features.

---

It's unusual to apply regularization to the intercept. If you omit the intercept regularization, the black classifier has lower regularization penalty. This isn't sufficient to permit us to draw any conclusions about which model, though, since we do not have information about out-of-sample generalization (or even about in-sample loss).

Answer 2

Regularization does not guarantee to reduce overfit.

Regularization reduces overfit in many cases because in these cases the real data model (e.g., physics models) have small weights. Reguarlization is a way to inject this knowledge in our model. It weeds out those models that have large weights, which tend to be models that overfit.

However, in simulation, you can definitely construct a model that have large weights and generate data from it. Regularization may not work well with this kind of data. Regularization will create a large bias in this case, I guess. But this kind of data is rare in real world.

The intuition what I think of is that not much weight is given to a particular feature. But isn't it sometimes necessary to focus on one feature (like in the above example x1)?

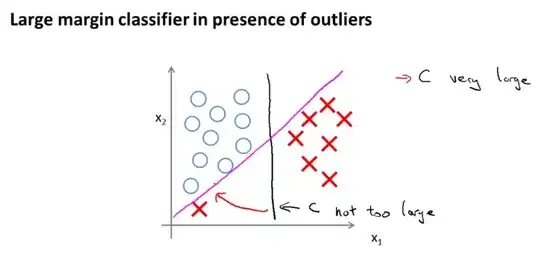
Edit: You can make the classifier give more weight to $x1$ by scaling $x1$ back by a factor of, say, 10. Then the black boundary will get very close to the magenta boundary. This is equivalent to discounting the component on the $x1$ dimension in the calculation of the Euclidean distance, but what makes the red cross on the left an outlier is largely because it is distant from the rest of the datapoints in the same class, in $x1$ dimension. By scaling $x1$ down, we are reducing the contribution of the outlier in the total loss.

Actually, we cannot tell from this example whether the magenta boundary is an overfit. This is the same as saying that we cannot be sure if the red cross on the bottom left is an outlier. We have to see other samples (like a test set) to be more certain.

Just for the sake of discussion, suppose we are sure that the red cross on the left is indeed an outlier. The problem, I believe, if not that we are not giving enough weight on one particular feature, it is that with a hard margin classifier, the decision boundary is sensitive to outliers, because most of the cost comes from one single datapoint. Regularization does not really help in this situation. A soft-margin classifier, which involves more datapoints in determining the decision boundary, will result in a boundary close to the one marked in black.