7

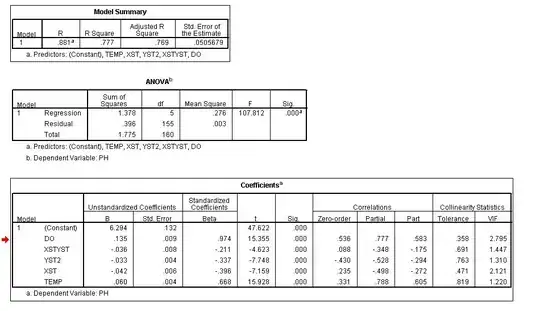
This is the result I've got after running linear regression analysis in SPSS: enter image description here

I am a bit confused why the sum of squared part correlations is not equal to (or less than) R squared, but rather exceeds the value of R squared (R squared = 77.7%, the sum of the squared part correlations = 88.6%).

Edit

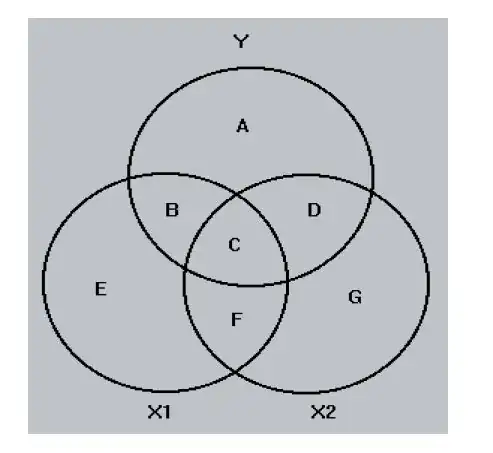
enter image description here

The variance of each variable is represented by a circle of unit area. Total area of Y covered by the X1 and X2 areas represents the proportion of Y's variance accounted for by the two independent variables (areas B,C and D). B and D are portions of Y that overlap uniquely by X1 and X2. The area C is the overlap of both X1 and X2 with Y. The unique areas (B and D) are squared part correlation coefficient. The part correlation between Y and X1 from which the X2 have been removed - area B.

R squared is the amount of variance in the dependent variable explained by all variables together.

So, it sounds logical that the sum of the squared part correlation cannot exceed the value of R squared. Or I am wrong?

chl
  • 50,972
  • 18
  • 205
  • 364
Beka
  • 171
  • 2
  • 6
  • You may be interested in reading this: [does-it-make-sense-for-a-partial-correlation-to-be-larger-than-a-zero-order-correlation?](http://stats.stackexchange.com/questions/9930/). – gung - Reinstate Monica Aug 25 '12 at 20:51
  • Does the square of the part correlation for X1 represent the explained variance removed when you start with a model for Y with X1 and X2 in it and you remove X1? If so this is not necessarily the same as the variance explained by X1 when only X1 is contained in the model. Similarly if X1, X2 and X3 are all in the model the amount of explained variance removed when X1 us taken out may be different for what you get taking X1 out when only X1 and X2 are in the model. So I am not sure I see why you expect these squared part correlations to sum to less than R square. – Michael R. Chernick Aug 25 '12 at 22:17
  • @Beka - Actually I get .897 as the sum of the squared part correlations. I share your perplexity: the variance that can be uniquely accounted for by individual variables should amount to less than the total variance accounted for (which includes variance explained jointly by two or more predictors). Are these data you could make available? – rolando2 Aug 26 '12 at 03:01
  • 2
    http://www.nd.edu/~rwilliam/stats1/x93b.pdf describes an example like this and explains that the paradoxical effect is caused by negative correlations among the predictors. The piece also discusses the strange result of having part r's be larger than zero-order r's. I'm still not sure it's not a hoax, though. – rolando2 Aug 26 '12 at 03:45

1 Answers1

5

Your output shows strong suppressive activity. It can never be shown on a Venn diagram. A suppressor IV is a predictor which addition to the model raises $R^2$ greater than its own $r^2$ with the DV, because suppressor is correlated mostly with the error term in the model which lacks the supressor, rather than correlated with the DV. Now, we know that the increase in $R^2$ due to inclusion a IV is the part correlation of this IV in the model obtained. So, if the absolute value of part correlation is greater than the absolute value of zero-order correlation, that variable is a suppressor. In your last table we see, that 4 of 5 predictors are suppressors.

ttnphns
  • 51,648
  • 40
  • 253
  • 462
  • @ronaldo2 Thank you very much as well, the pdf on semipartial correlation explains it very well. – Beka Aug 26 '12 at 10:31
  • Ah, @rolando2, I see now. I missed your comment somehow. – ttnphns Aug 26 '12 at 10:45
  • @Beka - I'm still very curious to see the raw data, if that's possible. One thing I'd like to check is the sum of what SPSS computes for the partial eta-squareds in a unianova procedure. – rolando2 Aug 26 '12 at 16:33
  • @rolando2 Is it possible to send the data here somehow as a private message? – Beka Aug 27 '12 at 16:15
  • @Beka Why don't you leave a link to the data? Not only rolando2 might take interest. – ttnphns Aug 27 '12 at 16:38
  • +1 to ttnphns. @Beka, if you want to read more about suppressor variables, I wrote a little bit about it here: [x-and-y-are-not-correlated-but-x-is-significant-predictor-of-y-in-multiple-regression](http://stats.stackexchange.com/questions/33888/34016#34016); another (long, but) great resource is [this](http://luna.cas.usf.edu/~mbrannic/files/regression/Partial.html). – gung - Reinstate Monica Aug 28 '12 at 01:31
  • @gung Thanks for the link! I will go through it as it seems that having suppressors is a bit serious issue. – Beka Aug 28 '12 at 21:56
  • @ttnphns Sorry, but I cannot make the data available publicly as I do not have permission to disseminate them. – Beka Aug 28 '12 at 21:58