Why is best subset selection not favored in comparison to lasso?

Question

I'm reading about best subset selection in the Elements of statistical learning book. If I have 3 predictors $x_1,x_2,x_3$, I create $2^3=8$ subsets:

1. Subset with no predictors
2. subset with predictor $x_1$
3. subset with predictor $x_2$
4. subset with predictor $x_3$
5. subset with predictors $x_1,x_2$
6. subset with predictors $x_1,x_3$
7. subset with predictors $x_2,x_3$
8. subset with predictors $x_1,x_2,x_3$

Then I test all these models on the test data to choose the best one.

Now my question is why is best subset selection not favored in comparison to e.g. lasso?

If I compare the thresholding functions of best subset and lasso, I see that the best subset sets some of the coefficients to zero, like lasso. But, the other coefficient (non-zero ones) will still have the ols values, they will be unbiasd. Whereas, in lasso some of the coefficients will be zero and the others (non-zero ones) will have some bias. The figure below shows it better:

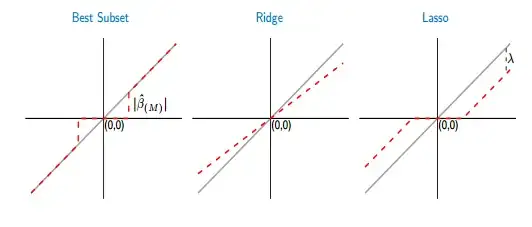
From the picture the part of the red line in the best subset case is laying onto the gray one. The other part is laying in the x-axis where some of the coefficients are zero. The gray line defines the unbiased solutions. In lasso, some bias is introduced by $\lambda$. From this figure I see that best subset is better than lasso! What are the disadvantages of using best subset?

Answer 1

In subset selection, the nonzero parameters will only be unbiased if you have chosen a superset of the correct model, i.e., if you have removed only predictors whose true coefficient values are zero. If your selection procedure led you to exclude a predictor with a true nonzero coefficient, all coefficient estimates will be biased. This defeats your argument if you will agree that selection is typically not perfect.

Thus, to make "sure" of an unbiased model estimate, you should err on the side of including more, or even all potentially relevant predictors. That is, you should not select at all.

Why is this a bad idea? Because of the bias-variance tradeoff. Yes, your large model will be unbiased, but it will have a large variance, and the variance will dominate the prediction (or other) error.

Therefore, it is better to accept that parameter estimates will be biased but have lower variance (regularization), rather than hope that our subset selection has only removed true zero parameters so we have an unbiased model with larger variance.

Since you write that you assess both approaches using cross-validation, this mitigates some of the concerns above. One remaining issue for Best Subset remains: it constrains some parameters to be exactly zero and lets the others float freely. So there is a discontinuity in the estimate, which isn't there if we tweak the lasso $\lambda$ beyond a point $\lambda_0$ where a predictor $p$ is included or excluded. Suppose that cross-validation outputs an "optimal" $\lambda$ that is close to $\lambda_0$, so we are essentially unsure whether p should be included or not. In this case, I would argue that it makes more sense to constrain the parameter estimate $\hat{\beta}_p$ via the lasso to a small (absolute) value, rather than either completely exclude it, $\hat{\beta}_p=0$, or let it float freely, $\hat{\beta}_p=\hat{\beta}_p^{\text{OLS}}$, as Best Subset does.

This may be helpful: Why does shrinkage work?

Answer 2

In principle, if the best subset can be found, it is indeed better than the LASSO, in terms of (1) selecting the variables that actually contribute to the fit, (2) not selecting the variables that do not contribute to the fit, (3) prediction accuracy and (4) producing essentially unbiased estimates for the selected variables. One recent paper that argued for the superior quality of best subset over LASSO is that by Bertsimas et al (2016) "Best subset selection via a modern optimization lens". Another older one giving a concrete example (on the deconvolution of spike trains) where best subset was better than LASSO or ridge is that by de Rooi & Eilers (2011).

The reason that the LASSO is still preferred in practice is mostly due to it being computationally much easier to calculate. Best subset selection, i.e. using an $L_0$ pseudonorm penalty, is essentially a combinatorial problem, and is NP hard, whereas the LASSO solution is easy to calculate over a regularization path using pathwise coordinate descent. In addition, the LASSO ($L_1$ norm penalized regression) is the tightest convex relaxation of $L_0$ pseudonorm penalized regression / best subset selection (bridge regression, i.e. $L_q$ norm penalized regression with q close to 0 would in principle be closer to best subset selection than LASSO, but this is no longer a convex optimization problem, and so is quite tricky to fit).

To reduce the bias of the LASSO one can use derived multistep approaches, such as the adaptive LASSO (where coefficients are differentially penalized based on a prior estimate from a least squares or ridge regression fit) or relaxed LASSO (a simple solution being to do a least squares fit of the variables selected by the LASSO). In comparison to best subset, LASSO tends to select slightly too many variables though. Best subset selection is better, but harder to fit.

That being said, there are also efficient computational methods now to do best subset selection / $L_0$ penalized regression, e.g. using the adaptive ridge approach described in the paper "An Adaptive Ridge Procedure for L0 Regularization" by Frommlet & Nuel (2016). Note that also under best subset selection you'll still have to use either cross validation or some information criterion (adjusted R2, AIC, BIC, mBIC...) to determine what number of predictors gives you the best prediction performance / explanatory power for the number of variables in your model, which is essential to avoid overfitting. The paper "Extended Comparisons of Best Subset Selection, Forward Stepwise Selection, and the Lasso" by Hastie et al (2017) provides an extensive comparison of best subset, LASSO and some LASSO variants like the relaxed LASSO, and they claim that the relaxed LASSO was the one that produced the highest model prediction accuracy under the widest range of circumstances, i.e. they came to a different conclusion than Bertsimas. But the conclusion about which is best depends a lot on what you consider best (e.g. highest prediction accuracy, or best at picking out relevant variables and not including irrelevant ones; ridge regression e.g. typically selects way too many variables but the prediction accuracy for cases with highly collinear variables can nevertheless be really good).

For a very small problem with 3 variables like you describe it is plain clear best subset selection is the preferred option though.