A generalization of the question asks for the distribution of $Y = \lfloor X/m \rfloor$ when the distribution of $X$ is known and supported on the natural numbers. (In the question, $X$ has a Poisson distribution of parameter $\lambda = \lambda_1 + \lambda_2 + \cdots + \lambda_n$ and $m=n$.)
The distribution of $Y$ is easily determined by the distribution of $mY$, whose probability generating function (pgf) can be determined in terms of the pgf of $X$. Here's an outline of the derivation.
Write $p(x) = p_0 + p_1 x + \cdots + p_n x^n + \cdots$ for the pgf of $X$, where (by definition) $p_n = \Pr(X=n)$. $mY$ is constructed from $X$ in such a way that its pgf, $q$, is
$$\eqalign{q(x) &=& \left(p_0 + p_1 + \cdots + p_{m-1}\right) + \left(p_m + p_{m+1} + \cdots + p_{2m-1}\right)x^m + \cdots + \\&&\left(p_{nm} + p_{nm+1} + \cdots + p_{(n+1)m-1}\right)x^{nm} + \cdots.}$$
Because this converges absolutely for $|x| \le 1$, we can rearrange the terms into a sum of pieces of the form
$$D_{m,t}p(x) = p_t + p_{t+m}x^m + \cdots + p_{t + nm}x^{nm} + \cdots$$
for $t=0, 1, \ldots, m-1$. The power series of the functions $x^t D_{m,t}p$ consist of every $m^\text{th}$ term of the series of $p$ starting with the $t^\text{th}$: this is sometimes called a decimation of $p$. Google searches presently don't turn up much useful information on decimations, so for completeness, here's a derivation of a formula.
Let $\omega$ be any primitive $m^\text{th}$ root of unity; for instance, take $\omega = \exp(2 i \pi / m)$. Then it follows from $\omega^m=1$ and $\sum_{j=0}^{m-1}\omega^j = 0$ that
$$x^t D_{m,t}p(x) = \frac{1}{m}\sum_{j=0}^{m-1} \omega^{t j} p(x/\omega^j).$$
To see this, note that the operator $x^t D_{m,t}$ is linear, so it suffices to check the formula on the basis $\{1, x, x^2, \ldots, x^n, \ldots \}$. Applying the right hand side to $x^n$ gives
$$x^t D_{m,t}[x^n] = \frac{1}{m}\sum_{j=0}^{m-1} \omega^{t j} x^n \omega^{-nj}= \frac{x^n}{m}\sum_{j=0}^{m-1} \omega^{(t-n) j.}$$
When $t$ and $n$ differ by a multiple of $m$, each term in the sum equals $1$ and we obtain $x^n$. Otherwise, the terms cycle through powers of $\omega^{t-n}$ and these sum to zero. Whence this operator preserves all powers of $x$ congruent to $t$ modulo $m$ and kills all the others: it is precisely the desired projection.
A formula for $q$ follows readily by changing the order of summation and recognizing one of the sums as geometric, thereby writing it in closed form:
$$\eqalign{
q(x) &= \sum_{t=0}^{m-1} (D_{m,t}[p])(x) \\
&= \sum_{t=0}^{m-1} x^{-t} \frac{1}{m} \sum_{j=0}^{m-1} \omega^{t j} p(\omega^{-j}x ) \\
&= \frac{1}{m} \sum_{j=0}^{m-1} p(\omega^{-j}x) \sum_{t=0}^{m-1} \left(\omega^j/x\right)^t \\
&= \frac{x(1-x^{-m})}{m} \sum_{j=0}^{m-1} \frac{p(\omega^{-j}x)}{x-\omega^j}.
}$$
For example, the pgf of a Poisson distribution of parameter $\lambda$ is $p(x) = \exp(\lambda(x-1))$. With $m=2$, $\omega=-1$ and the pgf of $2Y$ will be
$$\eqalign{
q(x) &= \frac{x(1-x^{-2})}{2} \sum_{j=0}^{2-1} \frac{p((-1)^{-j}x)}{x-(-1)^j} \\
&= \frac{x-1/x}{2} \left(\frac{\exp(\lambda(x-1))}{x-1} + \frac{\exp(\lambda(-x-1))}{x+1}\right) \\
&= \exp(-\lambda) \left(\frac{\sinh (\lambda x)}{x}+\cosh (\lambda x)\right).
}$$
One use of this approach is to compute moments of $X$ and $mY$. The value of the $k^\text{th}$ derivative of the pgf evaluated at $x=1$ is the $k^\text{th}$ factorial moment. The $k^\text{th}$ moment is a linear combination of the first $k$ factorial moments. Using these observations we find, for instance, that for a Poisson distributed $X$, its mean (which is the first factorial moment) equals $\lambda$, the mean of $2\lfloor(X/2)\rfloor$ equals $\lambda- \frac{1}{2} + \frac{1}{2} e^{-2\lambda}$, and the mean of $3\lfloor(X/3)\rfloor$ equals $\lambda -1+e^{-3 \lambda /2} \left(\frac{\sin \left(\frac{\sqrt{3} \lambda }{2}\right)}{\sqrt{3}}+\cos \left(\frac{\sqrt{3} \lambda}{2}\right)\right)$:
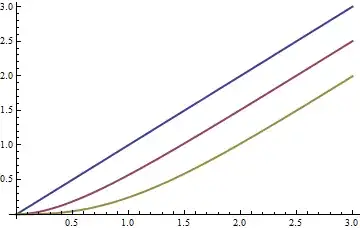
The means for $m=1,2,3$ are shown in blue, red, and yellow, respectively, as functions of $\lambda$: asymptotically, the mean drops by $(m-1)/2$ compared to the original Poisson mean.
Similar formulas for the variances can be obtained. (They get messy as $m$ rises and so are omitted. One thing they definitively establish is that when $m \gt 1$ no multiple of $Y$ is Poisson: it does not have the characteristic equality of mean and variance) Here is a plot of the variances as a function of $\lambda$ for $m=1,2,3$:
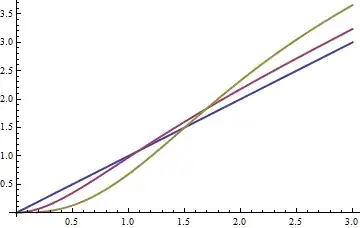
It is interesting that for larger values of $\lambda$ the variances increase. Intuitively, this is due to two competing phenomena: the floor function is effectively binning groups of values that originally were distinct; this must cause the variance to decrease. At the same time, as we have seen, the means are changing, too (because each bin is represented by its smallest value); this must cause a term equal to the square of the difference of means to be added back. The increase in variance for large $\lambda$ becomes larger with larger values of $m$.
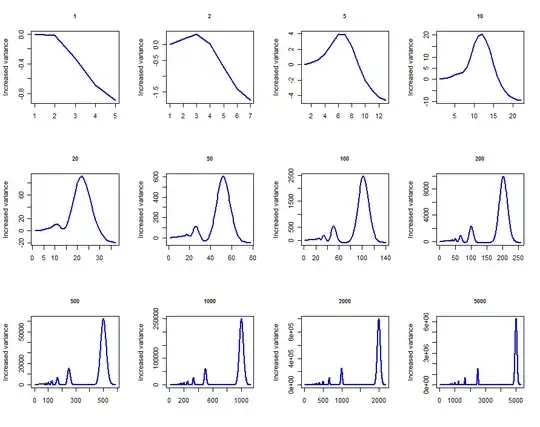
The behavior of the variance of $mY$ with $m$ is surprisingly complex. Let's end with a quick simulation (in R) showing what it can do. The plots show the difference between the variance of $m\lfloor X/m \rfloor$ and the variance of $X$ for Poisson distributed $X$ with various values of $\lambda$ ranging from $1$ through $5000$. In all cases the plots appear to have reached their asymptotic values at the right.
set.seed(17)
par(mfrow=c(3,4))
temp <- sapply(c(1,2,5,10,20,50,100,200,500,1000,2000,5000), function(lambda) {
x <- rpois(20000, lambda)
v <- sapply(1:floor(lambda + 4*sqrt(lambda)),
function(m) var(floor(x/m)*m) - var(x))
plot(v, type="l", xlab="", ylab="Increased variance",
main=toString(lambda), cex.main=.85, col="Blue", lwd=2)
})