1

I started to work with linear models recently and have a few questions about LMs and GLMs. My target looks like this (see below) and I have approx. 20 features. 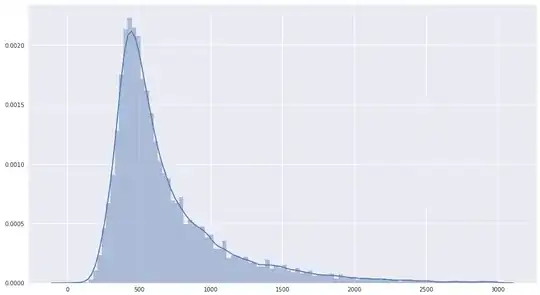enter image description here

Can somebody please confirm or answer my questions? Feel free to use the questions to test yourself.

  1. If I normalize my features before fitting an LM, I can say: the higher the absolute value of my regression coefficient, the more important is the feature?
  2. An LM is not a good choice because the target is not normally distributed?
  3. If two features are highly correlated I can delete one of them?
  4. If I have very strong correlated features, I should keep only one for fitting (multicollinearity)?
  5. If any of the correlation coefficients (e.g. pearson or kendall) is very close to zero between feature X and the target, I can delete it?
  6. Ẃhich link function and distribution should I assume for my GLM? I assume Poisson does not work since it is a discrete distributions and my values are continuous; a Gamma distribution can work as long as I have no 0 in my targets?
Ferdi
  • 4,882
  • 7
  • 42
  • 62
N8_Coder
  • 123
  • 3
  • 1
    The marginal distribution of your response is not generally relevant; the model assumption relates to conditional distributions. A mix of a variety of conditional distributions might look very different from any of the individual conditionals (i.e. the histogram here tells you little about the suitability of the distributional model). This is addressed in many questions on site. – Glen_b Jun 08 '18 at 09:47
  • You say it is not important how my response variable is distributed? But is this not the reason to use GLMs? – N8_Coder Jun 08 '18 at 14:35
  • 1
    There's a distinction between the conditional distribution, $F(Y|x_1,x_2,...,x_p)$ and the marginal distribution $F(Y)$. GLMs have an assumption about which family in the exponential class we're dealing with, but it's an assumption about the *conditional distribution*, not the marginal distribution. When you look at a histogram, you're looking at the *marginal* density of the sample's response variable about which no specific assumption is made. It might look like almost anything. [This same error occurs frequently in regression as well, and has been corrected by many people on site.] – Glen_b Jun 09 '18 at 02:15
  • 1
    Consider the following setup: $X_i\sim \text{ Bin}(1,\frac12)$. $Y_i\sim \text{ Pois}(e^{2.3X_i})$. I suggest you try a simulation for this case. This is explicitly in the form of a Poisson GLM with log-link and with $\beta=(0,2.3)^\top$. The marginal distribution of $Y$ is very far from Poisson (indeed, it's distinctly bimodal). It's actually a 50-50 mixture of a Poisson with mean 1 and a Poisson with mean about 10. If you look at the distribution of $Y$ alone, you'd get the (correct) impression that $Y$ was not Poisson; yet the Poisson GLM is the data generating model. – Glen_b Jun 09 '18 at 03:08
  • 1
    Possible duplicate of [Assumptions of generalised linear model](https://stats.stackexchange.com/questions/32285/assumptions-of-generalised-linear-model) – kjetil b halvorsen Jun 27 '18 at 09:32

0 Answers0