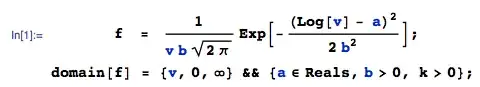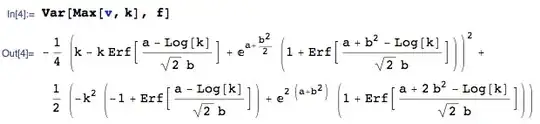Need handy formula for $Var[\max(V, K)]$

Question

In Appendix 12A, p. 262 of this book, the author Hull derives a handy, tractable formula for the expression $E[\max(V-K, 0)]$, where $V$ is a lognormally distributed random variable and $K$ is a constant.

I would like to see if a similarly handy formula can be derived for $Var[\max(V-K, 0)]$.

I know that if I can just somehow use Hull's approach to find $E[\max(V-K, 0)^2]$ then I could find $Var[\max(V-K, 0)]$, but I am stuck.

Actually, what I am really interested in is $E[]$ and $Var[]$ of $\max(V, K)$, but I can probably figure this out if you can help me with the $\max(V-K, 0)$ case.

Answer 1

The calculation of the expectation $E[max(V-k,0) ]$ is the value of a call option, prior to discounting for time.

To answer your question, it is given that $V \sim \text{Lognormal}(a,b)$ with pdf $f(v)$:

Then, you seek:

and

where:

• Expect and Var are the expectation and variance functions from the mathStatica package for Mathematica, which I am using to automate the calculation;
• Erf[z] denotes the error function $\text{erf}(z)=\frac{2}{\sqrt{\pi }}\int _0^z e^{-t^2} d t$, and where the cdf of a standard Normal variable is given by $\frac{1}{2} \left(1+\text{erf}\left(\frac{z}{\sqrt{2}}\right)\right)$;
• and making the substitution $c = \frac{a-\log (k)}{\sqrt{2} b}$ will make the result look neater.

Answer 2

Finding the first moment

Whenever I look up the Black-Scholes formula, I always worry about changing parameterizations and notations, so let's start off by reproducing the result in Hull's text. All of that work will be re-used to find the second moment.

Let $V \sim \text{lognormal}(\mu, \sigma^2)$. $\mu$ is the mean of $\log V$ (not the mean of $ V$!), and $\sigma^2$ is the variance of $\log V$. We'll also call $\phi$ the density of a standard normal random variate, and $\Phi$ its cdf.

\begin{align*} \mathbb{E}[\max(V−K,0)] &= \int_{K}^{\infty}(v-K)f(v)dv \\ &= \int_{K}^{\infty}v f(v)dv - K \mathbb{P}(V>K) \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty}\exp(\mu + \sigma z) \phi(z) dz - K \mathbb{P}\left(Z > \frac{\log K - \mu}{\sigma}\right) \tag{1} \end{align*}

We used the change of variable with the inverse transformation $V = \exp(\mu + \sigma Z)$.

The second part will need to be written in terms of $\Phi$, but to get there, we need to change the order of the inequality. To do this, we a.) exploit the symmetry of $Z$'s density, and b.) we rearrange the formula for a moment generating function of a (non-standard) normal distribution: $\mu = \log \mathbb{E}[V] - \frac{\sigma^2}{2}$.

\begin{align*} \mathbb{P}\left(Z > \frac{\log K - \mu}{\sigma}\right) &= \mathbb{P}\left(Z < \frac{\mu - \log K }{\sigma}\right) \\ &= \Phi\left(\frac{\mu - \log K }{\sigma}\right) \\ &= \Phi\left(\frac{\log \mathbb{E}[V] - \frac{\sigma^2}{2} - \log K }{\sigma}\right) \\ &= \Phi\left(\frac{\log \frac{\mathbb{E}[V]}{K} - \frac{\sigma^2}{2} }{\sigma}\right). \end{align*}

Regarding the first integral in (1), you can't avoid writing out $z$'s density because you have to complete the square. You also have to use that same rearranged moment-generating function formula from above:

\begin{align*} \int_{\frac{\log K - \mu}{\sigma}}^{\infty}\exp(\mu + \sigma z) \phi(z) dz &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp(\mu + \sigma z) \exp\left[-\frac{z^2}{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{z^2 - 2\mu - 2\sigma z}{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{(z-\sigma)^2 - \sigma^2 - 2\mu }{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{(z-\sigma)^2 }{2} \right] \exp\left[\mu + \frac{\sigma^2}{2} \right] dz \\ &= \exp\left[\mu + \frac{\sigma^2}{2} \right] \mathbb{P}\left( Z + \sigma > \frac{\log K - \mu}{\sigma} \right) \\ &= \exp\left[\mu + \frac{\sigma^2}{2} \right] \Phi\left( \frac{- \log K + \mu}{\sigma} + \sigma \right) \\ &= \exp\left[\mu + \frac{\sigma^2}{2} \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{\sigma^2}{2} }{\sigma} \right) \end{align*}

Unfortunately, after we complete the square, even though $z$ is the dummy variable, which is typically reserved for standard normal random variables, we were integrating the density of a mean $\sigma$ random variable.

Putting these two things together, we confirm the result in Hull:

$$ \mathbb{E}[\max(V−K,0)] = \exp\left[\mu + \frac{\sigma^2}{2} \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{\sigma^2}{2} }{\sigma} \right) - K \Phi\left(\frac{\log \frac{\mathbb{E}[V]}{K} - \frac{\sigma^2}{2} }{\sigma}\right) $$

Finding the second moment

The second moment integral splits up into three terms, and two of them are ones we have already dealt with

\begin{align*} \mathbb{E}[\max(V−K,0)^2] &= \int_{K}^{\infty}(v-K)^2f(v)dv \\ &= \int_{K}^{\infty}(v^2-2vK + K^2)f(v)dv \\ &= \int_{K}^{\infty}v^2 f(v)dv - 2K \int_{K}^{\infty}v f(v)dv + K^2 \int_{K}^{\infty}f(v)dv \\ &= \int_{K}^{\infty}v^2 f(v)dv \\ &- 2 K\exp\left[\mu + \frac{\sigma^2}{2} \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{\sigma^2}{2} }{\sigma} \right)\\ &+ K^2 \Phi\left(\frac{\log \frac{\mathbb{E}[V]}{K} - \frac{\sigma^2}{2} }{\sigma}\right) \end{align*}

Fortunately, the new integral can be solved using the same two tools of the above integral: completing the square and using the change of variables $V = \exp(\mu + \sigma Z)$:

\begin{align*} \int_{K}^{\infty}v^2 f(v)dv &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty}\exp(2\mu + 2 \sigma z) \phi(z) dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp(2\mu + 2\sigma z) \exp\left[-\frac{z^2}{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{z^2 - 4\mu - 4\sigma z}{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{(z-2\sigma)^2 - 4\sigma^2 - 4\mu }{2} \right] dz \\ &= \int_{\frac{\log K - \mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left[-\frac{(z-2\sigma)^2 }{2} \right] \exp\left[2\mu + 2 \sigma^2 \right] dz \\ &= \exp\left[2\mu + 2 \sigma^2 \right]\mathbb{P}\left( Z + 2\sigma > \frac{\log K - \mu}{\sigma} \right) \\ &= \exp\left[2\mu + 2 \sigma^2 \right] \Phi\left( \frac{- \log K + \mu}{\sigma} + 2\sigma \right) \\ &= \exp\left[2\mu + 2 \sigma^2 \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{3}{2} \sigma^2 }{\sigma} \right). \end{align*}

Putting everything together:

\begin{align*} &\mathbb{E}[\max(V−K,0)^2] \\ &= \exp\left[2\mu + 2 \sigma^2 \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{3}{2} \sigma^2 }{\sigma} \right) \\ &- 2 K\exp\left[\mu + \frac{\sigma^2}{2} \right] \Phi\left( \frac{ \log\frac{\mathbb{E}[V]}{K} + \frac{\sigma^2}{2} }{\sigma} \right)\\ &+ K^2 \Phi\left(\frac{\log \frac{\mathbb{E}[V]}{K} - \frac{\sigma^2}{2} }{\sigma}\right) \end{align*}

You can also check the variance $$ \text{Var}[\max(V−K,0)] = \mathbb{E}[\max(V−K,0)^2] - \left( \mathbb{E}[\max(V−K,0)] \right)^2 $$ against Wolfie's great answer below.