12

I'm reading Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. Then I'm not able to figure out the difference between hard voting and soft voting in context to ensemble based methods.

I quote descriptions of them from the book. The first two images from the top are description for hard voting, and last one is for soft voting.

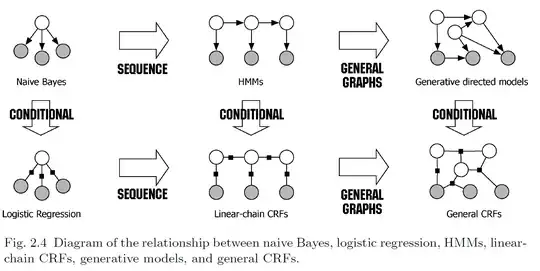
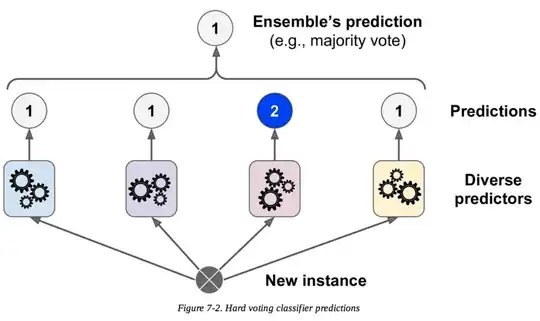
enter image description here

enter image description here

enter image description here

In my view hard voting is majority decision, but I don't understand soft voting and the reason why soft voting is better than hard voting. Would anyone teach me these?

a post I read

gogogogogo
  • 123
  • 1
  • 4
  • 1
    Please type out the text paragraph longhand and crop the text part out of the image, don't post image-as-text. This is important so that this question gets found by searching and indexing on important keywords like "hard voting gives more weight to highly confident votes". – smci Sep 05 '19 at 21:19

1 Answers1

18

Let's take a simple example to illustrate how both approaches work.

Imagine that you have 3 classifiers (1, 2, 3) and two classes (A, B), and after training you are predicting the class of a single point.

Hard voting

Predictions:

Classifier 1 predicts class A

Classifier 2 predicts class B

Classifier 3 predicts class B

2/3 classifiers predict class B, so class B is the ensemble decision.

Soft voting

Predictions

(This is identical to the earlier example, but now expressed in terms of probabilities. Values shown only for class A here because the problem is binary):

Classifier 1 predicts class A with probability 99%

Classifier 2 predicts class A with probability 49%

Classifier 3 predicts class A with probability 49%

The average probability of belonging to class A across the classifiers is (99 + 49 + 49) / 3 = 65.67%. Therefore, class A is the ensemble decision.

So you can see that in the same case, soft and hard voting can lead to different decisions. Soft voting can improve on hard voting because it takes into account more information; it uses each classifier's uncertainty in the final decision. The high uncertainty in classifiers 2 and 3 here essentially meant that the final ensemble decision relied strongly on classifier 1.

This is an extreme example, but it's not uncommon for this uncertainty to alter the final decision.

mkt
  • 11,770
  • 9
  • 51
  • 125