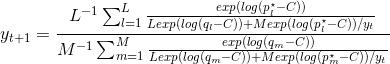Underflow when estimating marginal likelihood via bridge sampling

Question

I try to use an iterative procedure to estimate the marginal likelihood in a Bayesian setting for model selection. In case you are interested in the specifics of bridge sampling in my application, see this or this paper for instance. I'm fighting with numerical issues for quite some time now, so I thought I might as well give it a shot here and try my luck. I've tried to make what follows below as short, reproducible and general as possible.

The Setting

The goal is to run an iterative process of the form

to get an estimate for the marginal likelihood $y$ of my model (this iterative process will converge rather fast to some value for $y$). $L$ and $M$ are scalars. $p^{\star}_l$ and $p^{\star}_m$ is the nonnormalized posterior distribution evaluated in $l = 1,...,L$ importance density draws and $m = 1,...,M$ MCMC draws. $q_l$ and $q_m$ is the importance density evaluated in $l = 1,...,L$ importance density draws and $m = 1,...,M$ MCMC draws. Note that these are fixed values that are the result of evaluating a lot of log likelihoods and summing them up. The only term changing in each iteration is $y$. So basically I have the vectors $q_l$, $q_m$, $p^{\star}_l$ and $p^{\star}_m$ full of sums of thousands of log-likelihoods that I evaluate before running the iterative procedure above.

The Problem

The likelihood values used in the formula above are unfortunately not log-likelihoods (which I compute and store in the vectors), but actual likelihoods. This is the source of the numerical issues I have. You probably know the old problem of exponentiating negative log likelihoods that are large in magnitude. My log likelihoods are so negative that exp(log likelihood) will almost always be 0. There are some similar questions with answers already online, but none of those solutions did the trick for me.

What I tried

I think what might be promising is to exploit the fact that exp(log(x)) = x and expand the fraction, so you can rewrite above formula as

where C is a constant of your choice. For a proof that follows the same idea see the appendix of this paper. If one can find a suitable value of $C$ that makes the terms in the sum managable, the problem is solved. However, in my case $q_l$, $q_m$, $p^{\star}_l$ and $p^{\star}_m$ are very different in terms of magnitude, so no matter what value of $C$ I try to substract or add, I will end up with underflow or overflow again. Thus, right now I actually don't really know how to proceed from here. I appreciate any comment and tip.

Code and Data

You can find some example data (i.e. the vectors with the log likelihoods) here. The R code for the iterative process is

L <- 1000
M <- 5000
y <- numeric(length=100)
eval_downer <- numeric(length=L)
eval_upper <- numeric(length=M)
y[1] <- 0.5

for(t in 2:100){ 

  for(m in 1:M){
    up.m <- q_m[m]
    down.m <- (L * q_m[m]) + (M * p_m[m] / y[t-1])
    eval_downer[m]  <- up.m / down.m 
  }

  for(l in 1:L){
    up.l <- p_l[l]
    down.l <- (L * q_l[l]) + (M * p_l[l] / y[t-1])
    eval_upper[l]  <- up.l / down.l
  }

  upper <- mean(eval_upper)
  downer <- mean(eval_downer)

  y[t]  <-   upper / downer

  print(t)
}

Thank you!