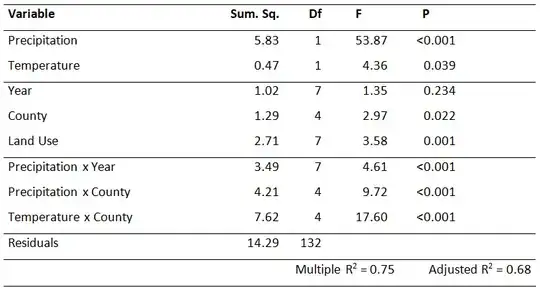
I'm testing the difference of a paired dataset. I need to select between sign test and Wilcoxon signed rank test. I have read from multiple sources that suggest using sign test if the distribution of difference is not a normal distribution under the null hypothesis. My distribution is a beta distribution (see figure), so I suppose that sign testshould be more powerful than signed rank test, but my power test suggests otherwise (signed rank test > sign test). Is there any idea why it happens? And should I select signed rank test? They gave very different results for significance test with very different power.
My difference boxplot looks like
I used the following code for power calculation:
power = function(group1, group2, reps = 1000, size = 36){
results <- sapply(1:reps, function(r){
group1.resample <- sample(group1, size = size, replace = T)
group2.resample <- sample(group2, size = size, replace = T)
# test <- wilcox.test(group1.resample, group2.resample, paired = T, exact = F)
# test <- SignTest(group1.resample, group2.resample)
test$p.value
})
sum(results < .05)/reps
}
# tested on n = 36
power(group1Data, group2Data, reps = 10000, size = 36)
Thanks!