I was reading this CrossValidated answer but the link provided no longer works. To avoid future irony, I'll reproduce the question and answer here:
What is the difference between linear regression on y with x and x with y?
There is a very interesting phenomenon about this topic. After exchanging x and y, although the regression coefficient changes, but the t-statistic/F-statistic and significance level for the coefficient don't change. This is also true even in multiple regression, where we exchange y with one of the independent variables.
It is due to a delicate relation between the F-statistic and (partial) correlation coefficient. That relation really touches the core of linear model theory. There are more details about this conclusion in my notebook: Why exchange y and x has no effect on p
For clarity, here's an example from simple regression to show what I'm talking about (in R):
data <- mvrnorm(n=100, mu=c(0.4, 2.15), Sigma=matrix(nrow=2, ncol=2, c(0.6, 0.34, 0.34, 0.81)), empirical=TRUE)
colnames(data) <- c("x", "y")
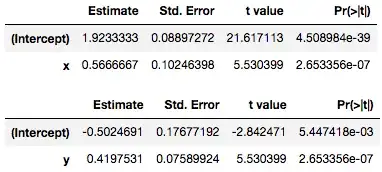
summary(lm(y ~ x, data))$coefficients
summary(lm(x ~ y, data))$coefficients
Which produces: