0

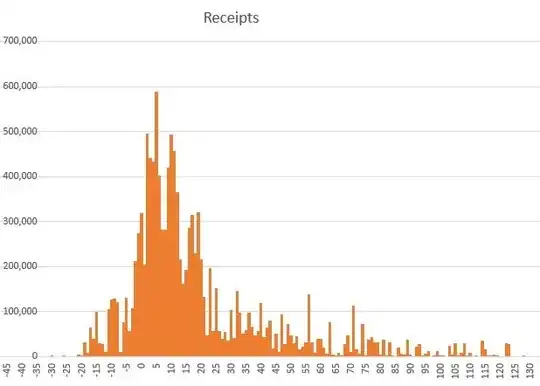
I have the following distribution of payment receipts with respect to their due date. Anything less than zero is prepaid and after zero is late. How should I formulate my basic approach to modelling the distribution of lateness?

I have considered a log normal model, but this would not work with the prepayments with a negative due difference. It is too skewed to use a normal distribution (M3 = 1.78) and the excess kurtosis is 3.54 (M4 = 6.54). I've also considered a Gaussian smoothing algorithm, but this is far too slow (10,000's of payments would need to be iterated over 100,000s of times for my purposes). Therefore, I'm looking to model this with a continuous function that is not an infinite sequence.

The goal is to compute a discrete probability for each number of days late (or early) for a future payment due.

Receipt Distribution

American Luke
  • 101
  • 2
  • You could try a skew-normal or skew-t distribution – kjetil b halvorsen May 22 '18 at 05:56
  • Hm. I also need to be able to control the kurtosis. In addition, my software package does not support the error function, so any model that relies on that would be hard to replicate with the desired accuracy. – American Luke May 22 '18 at 12:55
  • 1
    What is then your software? skew-t can take care of kurtosis. Here is a similar question with answer: https://stats.stackexchange.com/questions/338868/fitting-a-distribution-to-skewed-data-with-negative-values/340669#340669 – kjetil b halvorsen May 22 '18 at 12:57
  • Power BI (DAX). I also need to be able to create a cdf (not pdf). Looking on wikipedia, I only see pdf equations though. – American Luke May 22 '18 at 12:58

0 Answers0