6

Let $X_1, \dots, X_n$ be iid. $\text{Uniform}[-\theta,\theta]$. I need to find the complete sufficient statistic for $\theta$ or prove there does not exist such.

I know that $T = (X_{(1)}, X_{(n)} )$ is a sufficient statistic for $\theta$ but it is not a complete sufficient statistic.

I want to prove it. So first I tried to use the Basu's theorem . But in this case $R = X_{(n)} - X_{(1)}, $ is not an ancillary statistic.

So I tried prove using the definition of the complete sufficient statistic.

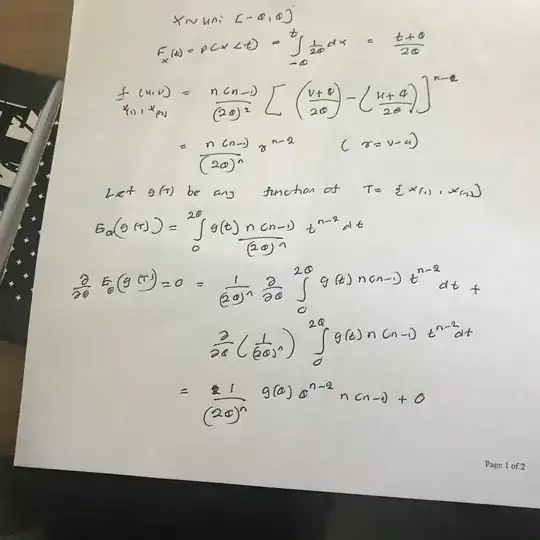
Here I have attached my work so far: enter image description here

But by doing like this , seems like that I am going to prove that $T$ is a complete sufficient statistic.

So can someone help to figure it out what I did incorrectly ?

The Pointer
  • 1,064
  • 13
  • 35
Sam88
  • 328
  • 3
  • 10
  • Since $T$ is a two-dimensional statistic, the expected value will need to be a double integral for arbitrary $g(T)$. – knrumsey May 18 '18 at 00:40
  • is it necessary ? because i found the joint distribution of $X_{(1)}$ and $X_{(n)}$. – Sam88 May 18 '18 at 00:42
  • Yes it is still necessary. By defintion, $E(g(X,Y)) = \int_x \int_y g(x,y)f(x,y)dx \ dy$ where $f(x,y)$ is the joint distribution. That's where you're going wrong. – knrumsey May 18 '18 at 00:44
  • Since $\theta$ is a scale parameter, you need to find a function of $(X_{(1)},X_{(n)})$ that is scale free... – Xi'an Oct 12 '18 at 18:07
  • For instance, $X_{(1)}/X_{(n)}$! – Xi'an Oct 12 '18 at 18:08
  • @Xi'an But I wanted to know how to compute it properly that's what I am trying in comments in knrumsey's answer. Could you help me in my approach ? – Daman Oct 12 '18 at 18:14
  • There is no generic approach to find an ancillary transform of a sufficient statistic, I believe. – Xi'an Oct 12 '18 at 19:02
  • A complete sufficient statistic like $$\max(-X_{(1)},X_{(n)})=\max_{1\le i \le n} |X_i|$$ does exist though. – StubbornAtom Oct 12 '18 at 19:24
  • Sufficiency of the above statistic is shown [here](https://stats.stackexchange.com/questions/354893/sufficient-statistics-for-uniform-%CE%B8-%CE%B8?noredirect=1&lq=1). And since $|X_i|\sim U(0,\theta)$, that $\max |X_i|$ is complete is [well-known](https://math.stackexchange.com/questions/699997/complete-statistic-uniform-distribution?noredirect=1&lq=1). – StubbornAtom Oct 13 '18 at 05:50
  • @StubbornAtom I haven't done topic Ancillary. I am just trying to prove why this is not complete. Can you look at my comments in knrumsey's answer. I am not able to understand how do we prove completeness for two-dimensional random sufficient statistics. – Daman Oct 13 '18 at 12:40
  • See related: https://stats.stackexchange.com/questions/354893/sufficient-statistics-for-uniform-theta-theta, https://stats.stackexchange.com/questions/360725/finding-maximum-likelihood-estimator-symmetric-uniform-distribution – kjetil b halvorsen Dec 05 '19 at 02:48

2 Answers2

4

Recall:

Definition: A statistic $T$ is complete for $\theta$ if $$E(g(T)) = 0, \ \text{ for all $\theta$} \quad \Rightarrow \quad P(g(T) = 0) = 1, \ \text{ for all $\theta$}$$

The part about $P(g(T) = 0) = 1$ basically says that the function $g$ is trivially $0$ everywhere (except possibly on a set of measure 0).

So... If you want to prove that $T$ is NOT complete, you can try to find a non-trivial function $g(T)$ for which $E(g(T)) = 0$ for all values of $\theta$.

Hint: Can you find $E(X_{(1)})$ and $E(X_{(n)})$? Start with that, and then try looking at linear combinations of the sufficient order statistics.

knrumsey
  • 5,943
  • 17
  • 40
  • This is what i exactly tried to do. But somehow i am not getting the desired answer. (please check the solution that i attached). So i am trying to figuring out that. – Sam88 May 18 '18 at 00:40
  • See my comment above. In this case, you can use $g(T)$ which is just a linear combination of the min and max. This saves you from having to integrate. – knrumsey May 18 '18 at 00:42
  • You are suggesting the about finding an ancillary statistic isnt it ? – Sam88 May 18 '18 at 00:48
  • No. We are using the definition of completeness directly. To prove that $T$ **is** complete, you have to show the condition for EVERY $g(T)$. To prove that $T$ is **not** complete, you just need to find one $g(T)$ that violates the condition. In this case, the $g(T)$ is very simple. So again, i suggest looking at linear combinations. – knrumsey May 18 '18 at 00:55
  • okay i will try that. But i have question. The order statistics are dependent isn't it ? so can we take expectations separately like you mentioned and find a linear combination ? Also do you think that basu's theorem can apply for this ? if that is so, then our life will be so much easy. – Sam88 May 18 '18 at 01:00
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/77667/discussion-between-knrumsey-and-sam88). – knrumsey May 18 '18 at 01:05
  • 1
    @knrumsey $E(X_1)=\frac{\theta}{n+1}$ , $E(X_n)=\frac{n\theta}{n+1}$ now how do I proceed I don't get it you said comput these values but how does that help in $E(g(X,Y)) = \int_x \int_y g(x,y)f(x,y)dx \ dy$ how do I use them here ? – Daman Oct 12 '18 at 17:09
  • 1
    @knrumsey $E((-n)g(x)X_1)+E(g(x)X_n)=0$ This makes it valid to say it's not complete isn't it ? – Daman Oct 12 '18 at 17:22
  • @Damn1o1 I'm a bit confused by your notation in the second comment, but it seems like you're on the right track. Set $g(T) = -nX_{(1)} + X_{(2)}$. So $g(T)$ is non trivial (not almost surely equal to $0$), but $E(g(T)) = 0$ for all values of $\theta$. So yes that would imply that $T$ is not complete. – knrumsey Oct 16 '18 at 21:50
  • I don't think $E(X_{(n)})=\frac{n\theta}{n+1}$. $E(X_{(n)})=\frac{n\theta}{n+1}$ holds for $U(0,\theta)$ but not $U(-\theta,\theta)$. – Tan Jan 06 '21 at 17:39
0

Method 1

$(X_{(1)},X_{(n)})$ is not complete because we can find $g\neq0$ but $\mathbb{E}\left[g(X_{(1)},X_{(n)})\right]=0,\forall\theta$. $g$ is $(t_1,t_2)\rightarrow\frac{n+1}{n-1}t_2-\frac{n+1}{1-n}t_1$.

This is because $\mathbb{E}(X_{(n)})=\frac{n-1}{n+1}\theta$ and $\mathbb{E}(X_{(1)})=\frac{1-n}{n+1}\theta$. Thus $\mathbb{E}\left[g(X_{(1)},X_{(n)})\right]=\mathbb{E}\left[\frac{n+1}{n-1}X_{(n)}-\frac{n+1}{1-n}X_{(1)}\right] = \frac{n+1}{n-1}\mathbb{E}(X_{(n)})-\frac{n+1}{1-n}\mathbb{E}(X_{(1)}) = \theta-\theta=0,\forall \theta$.

Method 2

If the sufficient statistic $(X_{(1)},X_{(n)})$ is complete, then it is a minimal sufficient statistic. However, (X_{(1)},X_{(n)}) is not a minimal sufficient statistic. A minimal sufficient statistic is $\max\{-X_{(1)},X_{(n)}\}$. It is possible that $(x_{(1)},x_{(n)})\neq(y_{(1)},y_{(n)})$ but $\max\{-x_{(1)},x_{(n)}\}=\max\{-y_{(1)},y_{(n)}\}$.

Tan
  • 1,349
  • 1
  • 13