How to correctly represent difference variables in DAGs?

Question

If I am interested in the causal effects of the change in a variable ($E$) on some outcome ($O$), how would I represent that in a directed acyclic graph (DAG)?

Suppose $\Delta E_2 = E_2 - E_1$, where $E_1$ & $E_2$ happen at times 1 & 2, would a correct DAG be:

1. Assuming that $\Delta E_2$ is simply captured by all levels of $E_1$ and $E_2$ (a la the same way interaction effects are so captured)?

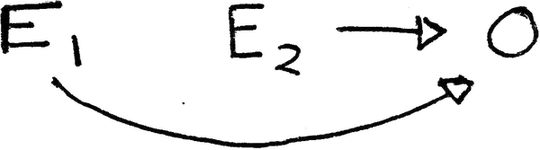
2. Assuming that $\Delta E_2$ is a causally distinct variable from $E_1$ and $E_2$, but requiring the presence of those variables?

3. Assuming that $\Delta E_2$ is independent of $E_1$ & $E_2$ and the latter are not necessary to represent the effects of $\Delta E_2$?

4. Something else?

NOTE: "DAG" does not mean "any old kind of causal or correlational graph," but is a tightly proscribed formalism representing causal beliefs.

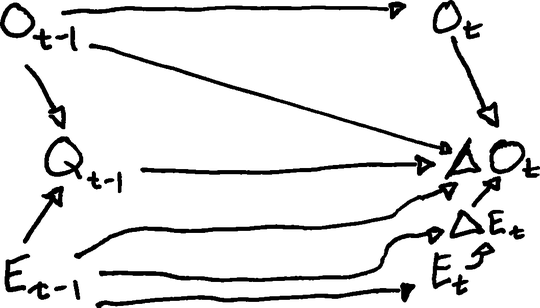
My motivation is that I am trying to think about DAG representation of dynamic models like the generalized error correction model:

$$\Delta O_t = \beta_{0} + \beta_{\text{c}}\left(O_{t-1} - E_{t-1}\right) + \beta_{\Delta E}\Delta E_{t} + \beta_E E_{t-1} + \varepsilon_t$$

Of course, the raw parameter estimate get transformed to interpret model as below, so perhaps DAGing the above model would be even messier?

Short-run instantaneous effect of change in $E$ on $\Delta O$: $\beta_{\Delta E}$

Short-run lagged effect of level of $E$ on $\Delta O$: $\beta_{E} - \beta_{\text{c}} - \beta_{\Delta E}$

Long-run equilibrium effect of lagged $E$ on $\Delta O$: $\frac{\beta_{\text{c}} - \beta_{E}}{\beta_{\text{c}}}$

Answer 1

The solution is to think functionally.

The value of $\Delta E_{2} = f(E_{1},E_{2})$ more specifically$ \Delta E_{2} = E_{2} - E_{1}$. Therefore difference variables may be represented in DAGs by option 4, "something else" (this DAG assumes $E_{1}$ and $E_{2}$ directly cause $O$ in addition to their difference):

If $E_{1}$ & $E_{2}$ do not have direct effects on $O$, $\Delta E_{2}$ still remains a function of its parents:

If we rewrite the single lag generalized error correction model thus ($Q_{t-1}$ for 'eQuilibrium term', where $Q_{t-1} = O_{t-1} - E_{t-1}$):

$$\Delta O_t = \beta_{0} + \beta_{\text{c}}\left(Q_{t-1}\right) + \beta_{\Delta E}\Delta E_{t} + \beta_E E_{t-1} + \varepsilon_t$$

Then the DAG underlying the model for $\Delta O_{t}$ (ignoring its descendants at $t+1$) is:

The effects of $E$ on $\Delta O_{t}$ from the model thus enter from equilibrium term $Q_{t-1}$, from $E_{t-1}$ and from change term $\Delta E_{t}$. Other causes of $O_{t-1}$, $O_{t}$, $E_{t-1}$ and $E_{t}$ (e.g., unmodeled variables, random inputs) are left implicit.

The portion of this answer corresponding to the first two DAGs is courtesy of personal communication with Miguel Hernán.

Answer 2

EDIT:

If you are only concerned with representing nonparametric relationships among your variables, I think 1) would be most appropriate. While there may be a more specific functional form relating the two variables to the outcome, in a DAG it is not necessary to represent that form. On the other hand, if you wanted to use a path diagram representing a linear structural equation model like the one you wrote, it would make sense to include the difference score in the diagram; this way, the specific model you wrote and the diagram would be equally specific. A DAG is more vague (but also more flexible) since it does not require (or necessary allow) for specific function form.

It might come down to the goal of drawing your DAG. If your goal is represent with as much precision as possible the relationships among your variables, it would make sense to include the difference term as its own variable since it does have its own causal force. A graph without it would also be valid. You could, in theory, make the same conditional independence statements about the outcome and the predictors with a more detailed DAG than with a less detailed one.

---

My intuition is closest to 3). If it's true that $E_1$ and $E_2$ do not directly affect $O$ except through their difference, then 3) is correct, and I would add edges from $E_1$ and $E_2$ to $\Delta E_2$ and from $E_1$ to $E_2$ for completeness. No other nodes would point to the difference variable, but variables that predict the difference would point instead to $E_1$ and/or $E_2$. Graphically, what I'm describing is:

E1
 |---->  E2-E1 ---> O
 V       ^
E2-------|

with possible additional arrows from $E_1$ and $E_2$ to $O$ if they affect $O$ beyond their effect through their difference.