I am implementing a Tobit model, since my dependent variable (educational expenditure shares) is left-censored at 0.
Below you'll find a swarmplot of the dependent variable and the explanatory variable of interest (gender specific bargaining power converted to dummies: 1 for male; 2 for female; 3 for mixed).
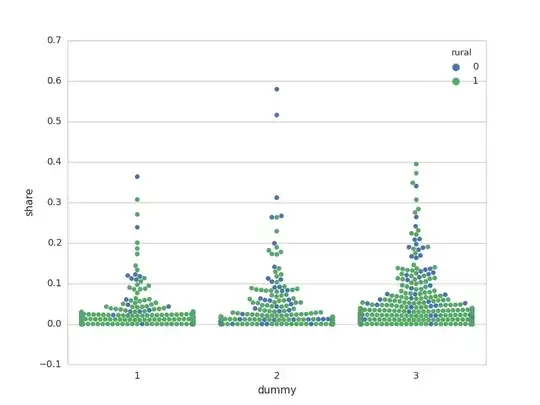
Aa you can see I have some large outliers I would like to drop. Naturally I can just identify them in my dataset and delete the observations. However, since I am using the Tobit model, which also allows for right-censoring (two-limit-Tobit model) I was wondering if I could just set the right-sided limit f.e at 0.35 and thereby drop the outliers? I thought about this: \begin{align} y_i = \begin{cases} y^*_i & \text{if } 0 < y^*_i < 0.35\\ 0 & \text{if } y^*_i \leq 0 \end{cases} \end{align} I have the feeling that this would have a different implication as I understood that the truncated Tobit model "drops" observations. Could I then truncate from above, censor from below? Or is this in general a bad idea?