4

I am a beginner of machine learning, and I just studied Linear Regression. $$h(x) = \sum_{i=0}^n \theta_i x_i$$ By finding the minimum values of $\theta$ via Gradient descent or Normal equation, we could get the equation of $h(x)$ to solve the problem, or make the hypothesis of a price of real estate, or classify the area by a price.

After I referred Recurrent neural network in wikienter image description here

I find it's hard to relate the equation $h(x)$ to neural network. I didn't the see the neural cells or the network. There only is an equation, using equation could solve the application problem. But how to go further to the neural network?

Lerner Zhang
  • 5,017
  • 1
  • 31
  • 52
JustWe
  • 143
  • 1
  • 7
  • 1
    You do not find minimum values of $\theta$ but optimal values according to your collected data to solve your problem. – doubllle Apr 27 '18 at 12:00
  • @doubllle isn't the `optimal` means the value most approach to the line of the function $h(\theta)$ , when derivative of $h(\theta)$ equal to zero? – JustWe Apr 27 '18 at 12:15
  • No, you also do NOT take derivatives of $h(\theta, x)$ to get optimal values. $h(\theta, x)$ is the hypothetical function you use to estimate the real function governing your problem. You need to define objective function based on your $h(\theta, x)$ to get optimal values of \theta. Hopefully this is clear. – doubllle Apr 27 '18 at 12:39
  • And also the optimal $\theta$ would make the line of $h(\theta)$ approach the real line from which your data are generated. In other words, you try to minimize the total error between the line $h(\theta)$ and all data points to get the optimal values of $\theta$. – doubllle Apr 27 '18 at 12:45
  • @Jiu You have to express the loss function (that which is to be minimized) in terms of the model parameters, differentiate the expression with respect to those parameters, and then solve for those parameters by setting the differentiated expression to zero (for linear least squares). In principle, we'd like to do the same thing for neural networks but in general you won't be able to solve the differentiated loss for the parameter matrix in closed form (i.e., it will require iteration). – Josh Apr 27 '18 at 15:22

1 Answers1

0

it's hard to relate the equation h(x) to neural network.

linear regression contains a vector to be optimized/learned which can be also viewed as a projection from the input to the output. This process is kind of like the connections in our brain then it is called neural network.

I didn't the see the neural cells network, there only an equation, using equation could solve the application problem.

The cell also can be interpreted as the connection as the vector in the linear regression. Consider this, if a value in the vector makes a certain number in the input very large or vanishingly zero, then it just transmits or stops the information from the one side to the other.

But how to go further to the neural network?

RNN is a neural network much more complex than linear regression, because it contains many gates(non-linear transformation like tanh, also called activation function) and linear transformations. It also takes the information from the previous step into consideration.

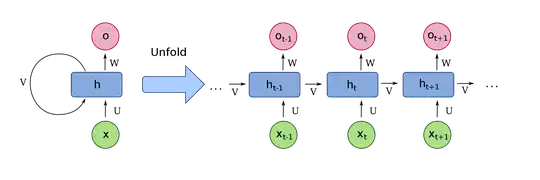
Let's unroll the RNN as requested in the comments:

As shown below, the blue and green circles are linear or non-linear transformations(actually activation or activation functions combined after linear transformation which is normally matrix multiplications for batched cases) and the f functions are some non-linear transformations. After we process the $x_i$ we put the output(with the normal input of the step $x_{i+1}$) to the cell in the next step $x_{i+1}$ and apply a non-linear transform to them and get the output of the step $x_{i+1}$ and so on.

Simplified illustration from here: https://deeplearning4j.org/lstm.html

enter image description here

Some shameless recommendations you may need:

Structure of Recurrent Neural Network (LSTM, GRU)
Is anyone stacking LSTM and GRU cells together and why?
Understanding LSTM units vs. cells

Lerner Zhang
  • 5,017
  • 1
  • 31
  • 52
  • The question & this answer are both confusing. I have no idea what *"linear regression contains a matrix to be optimized"*, or *"This process is kind of like the connections in our brain then it is called neural network"* means. – Josh Apr 27 '18 at 11:10
  • @Josh In linear regression variables to be optimized form a vetor. And the similarity between the true neural cells and artificial neural networks lie in the connections via which the information is processed. – Lerner Zhang Apr 27 '18 at 11:16
  • @Josh I am all ears, and you are very welcome to correct me. – Lerner Zhang Apr 27 '18 at 11:33
  • But your answer refers to a matrix -- with no mention of its dimensionality -- and now you are talking about a vector. That's very unclear. Moreover, the question leaps from linear least squares to recurrent neural networks. It seems like @Jiu is looking for a mathematical expression giving the predictions of a neural network in terms of its inputs and connection weights, which is actually pretty simple and generally consists of nested activation functions operating on the matrix product of weights and previous-layer outputs. – Josh Apr 27 '18 at 11:50
  • Perhaps a good approach would be to first figure out exactly what @Jiu is asking, and if the assumption in my prior comment is correct, show him the expression relating input, weights, and output for a specific feedforward network topology. Then explain how a recurrent network can be unrolled into feedforward form, and at that point he should be able to see how the expression generalizes to NNs in general, as opposed to only feedforward. – Josh Apr 27 '18 at 11:54
  • @ OK, I think your comments can supplement my answer above. I only have given the direction here. – Lerner Zhang Apr 27 '18 at 12:09
  • I would be very happy to see someone explaining how to unroll a RNN to FNN, giving all the gates and linear or nonlinear transforms. :)) – doubllle Apr 27 '18 at 12:57
  • @doubllle It ain't pretty. This paper contains some very simple examples. Of course, in the unrolled representation you wind up with a lot of connections constrained to have the same weight. https://arxiv.org/pdf/1506.00019.pdf – Josh Apr 27 '18 at 15:27
  • @doubllle I have appended the explanation as you requested. – Lerner Zhang Apr 28 '18 at 01:32
  • Thanks, great illustration for better understanding RNN! Thank @Josh as well for recommending the review paper. – doubllle Apr 28 '18 at 12:46