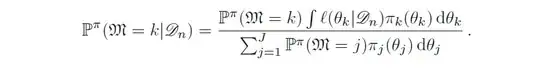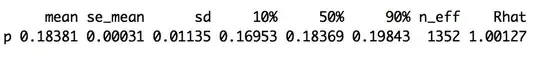I'm trying to use Stan and R to fit a model that, uhh, models the observed realisations $y_i = 16, 9, 10, 13, 19, 20, 18, 17, 35, 55$, which are from a binomial distributed random variable, say, $Y_i$, with parameters $m_i$ (the number of trials) and $p_i$ (probability of success). So we have $Y_i \sim (p_i, m_i)$ for $1 \le i \le 10$.
For the purposes of this experiment, I'm going to assume that all of the $m_i$ are fixed and given by $m_i = 74, 99, 58, 70, 122, 77, 104, 129, 308, 119$.
I'm going to use Jeffrey's prior: $\alpha=0.5$ and $\beta=0.5$.
I'm trying to
- Find the range of the $p_i$ (i.e., the parameters $r = \max\limits_{i = 1, \dots , 10} p_i - \min\limits_{i = 1, \dots , 10} p_i$).
- Plot the posterior density of $r$.
- Find a Bayesian estimate for $r$.
- Find the standard deviation of the posterior distribution of $r$.
I will be using Stan/RStan/R to do this.
My code for this is as follows:
```{r}
library(rstan)
library(bayesplot)
```
```{stan output.var="BinMod_beta"}
data {
int <lower = 1> mi[10];
int <lower = 0> yi[10];
real <lower = 0> alpha;
real <lower = 0> beta;
}
parameters {
real <lower = 0, upper = 1> p[10];
}
transformed parameters {
real r;
real mx = max(p);
real mn = min(p);
r = mx - mn;
}
model {
yi ~ binomial(mi, p);
p ~ beta(alpha, beta);
}
```
```{r}
data.in <- list(mi = c(74, 99, 58, 70, 122, 77, 104, 129, 308, 119), yi = c(16, 9, 10, 13, 19, 20, 18, 17, 35, 55), alpha = 0.5, beta = 0.5)
model.fit1 <- sampling(BinMod_beta, data=data.in)
```
```{r}
print(model.fit1, pars = c("p", "r"), probs=c(0.1,0.5,0.9), digits = 5)
```
```{r, out.width="0.8\\textwidth", fig.align='center'}
mcmc_areas(posterior, pars="r", point_est="mean")
```
My plot of the posterior density of $r$ is
I thought I had gone about this correctly, until I looked at the values I was getting:
The minimum value for $p_i$ in this table is $0.09535$, and the maximum value for $p_i$ in the table is $0.46167$. This would give us $r = 0.46167 - 0.09535 = 0.36632 \not= 0.37543$. So did I do something wrong here? I only recently started learning MCMC, simulations, and Stan, so it's not at all clear to me that I've done anything incorrectly.
I would greatly appreciate it if people could please take the time to to review this and provide feedback.
EDIT: Results of model with single $p$ instead of individual $p_i$s: