1

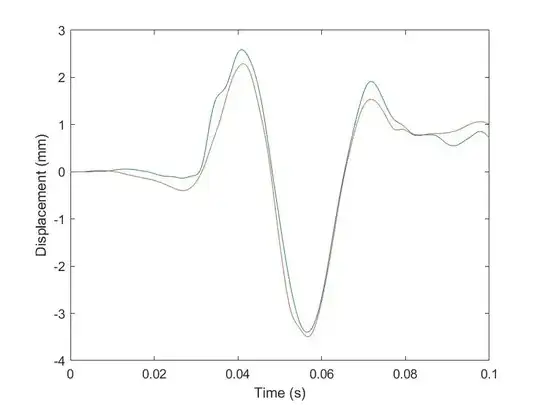
I am working on a project comparing the accuracy of two imaging techniques to measure displacement. I have attached a graph comparing the displacement measured by both techniques over time.

enter image description here

I am looking for a method to quantify the similarity of these two plots, preferably using Matlab. I have tried the 2-sample Kolmogorov–Smirnov which was unsuccessful. I have also tried cross-correlation which gives a strong positive correlation between the two plots however as the data is non-stationary I believe this could be over-stated due to auto-correlation.

My current solution is to use Spearman's rank to show similarity in magnitudes of the plots partnered with RMS error to show that they are in phase. However, I do not believe this would be a 'proper' way to achieve my goal. Is there a more appropriate statistical test I can use to quantify similarity of these plots of the two imaging techniques?

mkt
  • 11,770
  • 9
  • 51
  • 125
Stuart Boyd
  • 11
  • 3
  • 1
    In principle, Spearman rank is unsuitable. Consider that $y$ and $by, b > 0$, always have Spearman rank correlation of 1 regardless of $b$. So even perfect correlation doesn't guarantee identity. If you want to measure agreement with a single measure, use concordance correlation. I see no reason why you shouldn't extend that to concordance autocorrelation. – Nick Cox Apr 19 '18 at 09:39
  • 2
    Possible duplicate of [Does Spearman's $r = 0.38$ indicate agreement?](https://stats.stackexchange.com/questions/199678/does-spearmans-r-0-38-indicate-agreement) – Nick Cox Apr 19 '18 at 09:42
  • Search also for discussions of concordance correlation on CV. – Nick Cox Apr 19 '18 at 09:44
  • I'm not sure if that's a duplicate - there's certainly a similarity, but there's also some key differences. While the answer to both is "no" the proper alternative is different. – Peter Flom Apr 19 '18 at 12:06
  • There is a difference in $\Delta y$, there is a difference in magnitude. I would adjust for the differences before I look for similarity. First I would solve for min$||y1-m\,(y2-b)||$. Then look for similarity, e.g., R$^2$ or whatever. – Carl Apr 24 '18 at 03:21

0 Answers0