If you need to come up with confidence intervals for some kind of complicated estimator, then the most simple and generic approach is to use bootstrap. Same as with constructing confidence intervals for the kernel densities themselves, just re-sample your data many times, estimate the quantity of interest on the data and then calculate the empirical quantiles from this simulated data to get the interval of interest.
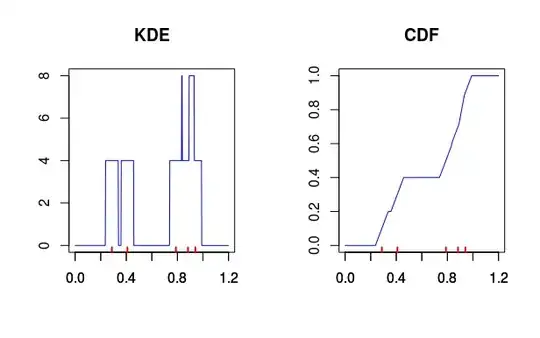
Sidenote: As noticed by me and Nick Cox in comments to your previous question, using kernel density to calculate the quantiles, especially the extreme ones, is generally a bad idea. To convince yourself, look at the plot of (very poor) kernel density estimate with rectangular kernel and accompanying cumulative distribution generated using it. It was estimated given five data points (red dots below). Notice that if you used it to compute the quantiles, then for the small quantiles, the function will return zeros for everything smaller then the lowest observed value minus the bandwidth you used for the kernel. The estimates would completely depend on the chosen bandwidth and the observed data and would tell you almost nothing about the values outside of the range of the observed values.
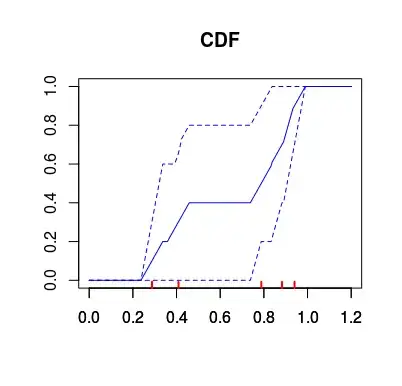
The above problems actually can be nicely illustrated when you calculate the bootstrap confidence intervals for the estimated distribution. As you can see below, the most uncertain values on the extremes, get the narrowest intervals, where the intervals outside the range of the data have zero width. So the estimate for the distribution would be "certain" that anything below 0.2 have zero probability of occurrence, while being completely wrong about it (the data was actually sampled from the standard uniform distribution).