Degree of alignment between judges (example: equestrian judges)

Question

When two equestrian judges are judging an equestrian event they each give their marks for every horse/rider combination in the event. Let's assume that there are 20 horses being judged. However, in comparing their scores, the judges might get a very poor correlation (eg. R<0) in terms of, say, the overall top-scoring, place-getting, 8 horses, (ie based on the average of both judges' scores), but they get a very high correlation (eg. R>0) in terms of their scoring of the remaining 12, low-scoring horses. As a result, the aggregate correlation coefficient (eg. R>0) might still well show that the two judges were "quite well aligned' in terms of their overall scoring of the event whereas we know that they did not correlate consistently if we were to analyse various subsets of data. So what conclusion can we make about the degree of "alignment" between these two judges (which is the key question we are trying to solve")? Can we still say that, over the entire data set "they are well aligned in their judging" or do we say that the data provides no conclusion as to their degree of alignment, given that there are significant differences in R in respect of various subsets of the data?!" Maybe the question might also be, if this is the sort of data we are looking at and trying to decide just how "aligned" the judges are in their scoring of the horses, is correlation the best statistic to use?

Answer 1

Thanks for the explanation of judging and the data example, which make the question helpfully concrete. I will label your judges A and B

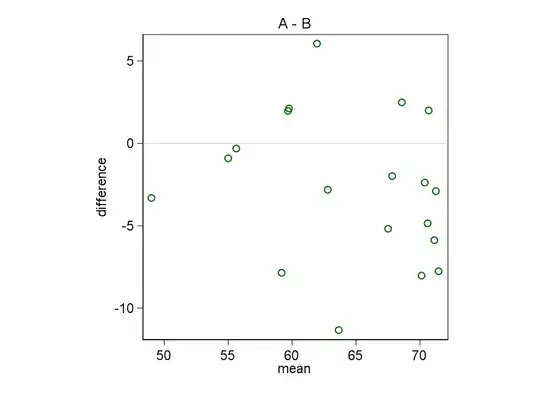
1. A helpful plot is difference A $-$ B versus mean (A + B)/2. In biostatistics especially this plot is often called the Bland-Altman plot after statisticians Martin Bland (1947- ) and Douglas Altman (1948- ). It has a longer history and was, for example, often mentioned by John W. Tukey (1915--2000) as a simple device. A natural reference line is A $-$ B = 0 corresponding to agreement A = B. Here is one such for your sample data.

2. I don't think it helps much to look for clusters in this plot or the more obvious scatter plot A versus B unless they really jump out at you. The risk of over-interpreting small clusters is probably greater than that of missing genuine fine structure.

3. A measure of agreement (rather than correlation) is concordance correlation, often attributed to Lin, who has made most of it, but explicit or implicit in earlier work by others. Here are some results from a Stata implementation for your data:

       Concordance correlation coefficient (Lin, 1989, 2000):
   
    rho_c   SE(rho_c)   Obs    [   95% CI   ]     P        CI type
    0.749     0.098      19     0.558  0.940    0.000   asymptotic
                                0.489  0.887    0.000  z-transform
   
   Pearson's r =  0.811  Pr(r = 0) = 0.000  C_b = rho_c/r =  0.923
   Reduced major axis:   Slope =     0.880   Intercept =     5.215
   
   Difference = A - B
   
           Difference                 95% Limits Of Agreement
      Average     Std Dev.             (Bland & Altman, 1986)
      -2.658       4.433                -11.347      6.031
   
   Correlation between difference and mean = -0.213
   
   Bradley-Blackwood F = 3.783 (P = 0.04374)
   

The concordance correlation is pulled below the Pearson correlation by any systematic differences between judges. Although just a single-number summary the concordance correlation is focused on measuring agreement, not correlation!

A paper of mine details here surveying this territory may be accessible to you. The examples from a different field should not be too distractingly alien: the principles here are generic.

Detail: The plot here uses jittering to shake identical points apart.