7

For 86 companies and for 103 days, I have collected (i) tweets (variable hbVol) about each company and (ii) pageviews for the corporate wikipedia page (wikiVol). The dependent variable is each company's stock trading volume (stockVol0). My data is structured as follows:

company  date  hbVol    wikiVol   stockVol0  comp1  comp2 ... comp89  marketRet
-------------------------------------------------------------------------------
1        1     200        150     2423325      1      0   ...   0     -2.50
1        2     194        152     2455343      1      0   ...   0     -1.45
.        .      .          .         .         .      .   ...   .
1       103    205        103     2563463      1      0   ...   0      1.90
2        1     752        932     7434124      0      1   ...   0     -2.50
2        2     932        823     7464354      0      1   ...   0     -1.45
.        .      .          .         .         .      .   ...   .
.        .      .          .         .         .      .   ...   .
86      103     3          55      32324       0      0   ...   1      1.90

As I understood, this is called pooled cross-sectional time series data. I have taken the Log-value of all variables to smoothen the big differences between companies. A regression model with both independent variables on the dependent stockVolo returns:

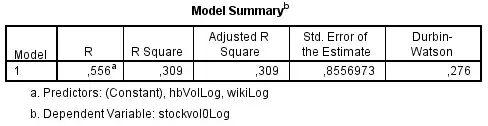
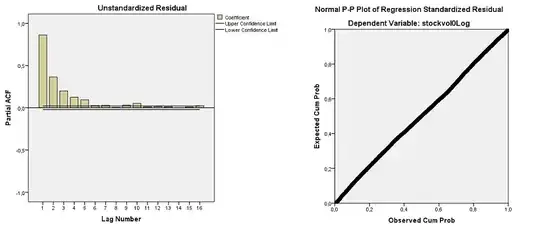
enter image description here

A Durbin-Watson of 0,276 suggest significant autocorrelation of the residuals. The residuals are, however, bellshaped, as can be seen from the P-P plot below. The partial autocorrelation function shows a significant spike at a lag of 1 to 5 (above upper limit), confirming the conclusions drawn from the Durbin-Watson statistic:

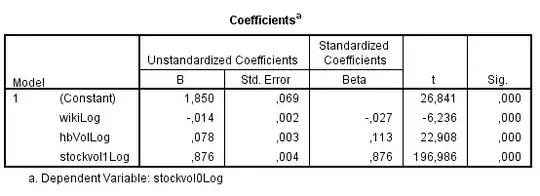
enter image description here

The presence of first-order autocorrelated residuals violates the assumption of uncorrelated residuals that underlies the OLS regression method. Different methods have been developed, however, to handle such series. One method I read about is to include a lagged dependent variable as an independent variable. So I created a lagged stockVol1 and added it to the model:

enter image description here

Now, Durbin-Watson is at an accceptable 2,408. But obviously, R-squared is extremely high because of the lagged variable, see also the coefficients below:

enter image description here

Another method I read about when being confronted with autocorrelation, is autoregression with Prais-Winsten (or Cochrane-Orcutt) method. Once performing this the model reads:

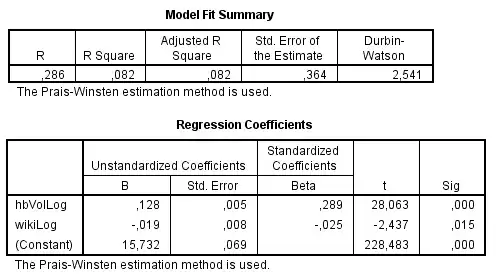
enter image description here

This is what I don't understand. Two different methods, and I get very different results. Other suggestions for analyzing this data include (i) not including a lagged variable but reformat the dependent variable by differencing (ii) perform AR(1) or ARIMA(1,0,0) models. I haven't calculated those because I am now lost on how to proceed because of the different results of the two tests I did perform.

What model should I use to perform a proper regression on my data? I'm very keen on understanding this, but have never had to analyze a timeseries dataset like this before.

Pr0no
  • 748
  • 7
  • 16
  • 28

4 Answers4

4

For each of the 86 companies , identify an appropriate ARMAX model which should incorporate the effects ( both contemporaneous and lag ) of the two user-suggested predictor variables and any necessary ARIMA structure. Incorporate any needed ( and empirically identifiable ) structure reflecting unspecified deterministic effects via Intervention Detection. Use these empirically identified intervention variables to cleanse the output series and remodel using the cleansed series as an ARMAX model. Now review the results for each of these 86 case studies and conclude about a common model. Estimate the common model both locally ( i.e. for each of the 86 companies ) and then estimate it globally ( all using the cleansed output series). Form an F test according to Gregory Chow http://en.wikipedia.org/wiki/Chow_test to test the null hypothesis of a common set of parameters across the 86 groups. If you reject the hypothesis then carefully examine the individual results ( 86 ) and conclude about which companies DIFFER from which companies. We have recently added this functionality to a new release of AUTOBOX, a piece of software that I am involved with as a developer. We are currently researching a formal way to find out ala Scheffe which companies differ from the others.

AFTER RECEIPT OF DATA:

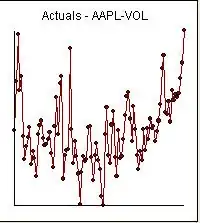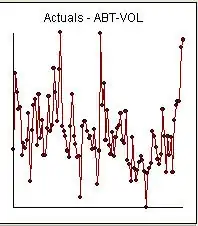The complete data enter link description hereset can be found at , I selected the first 3 companies (AA,AAPL,ABT). I selected trading volume (column S) as the dependent and the two predictors tweet (Z) and wiki (V) per the OP's suggestion. This selection can be found at enter link description here. 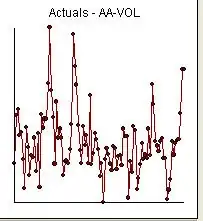Simple plots of the three dependent series suggest anomalies enter image description here and enter image description here and enter image description here . Since anomalies are present the appropriate regression needs to take into account these effects. 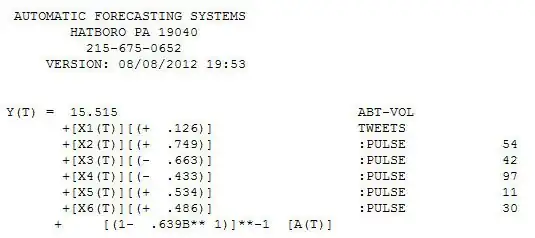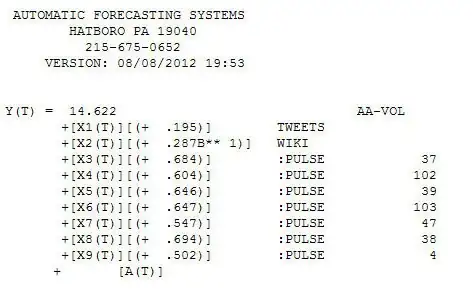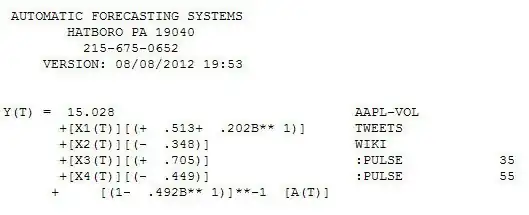Following are the three models ( including any necessary lag structures in the two inputs ) and the appropriate ARIMA structure obtained from an automatic transfer function run using AUTOBOX ( a piece of software I have been developing for the last 42 years )enter image description here and enter image description here and enter image description here . We now take the three cleansed series returned from the modelling process and estimate a minimally sufficient common model which in this case would be a comtemporary and 1 lag PDL on tweets and a contemporary PDL on wiki with an ARIMA of (1,0,0)(0,0,0). Estimating this model locally and globally provides insight as to the commonality of coefficients .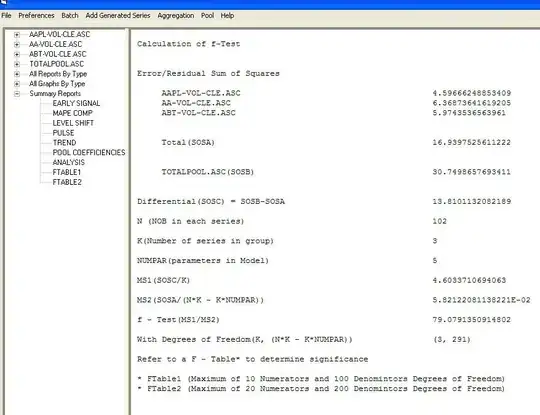enter image description here with coefficients 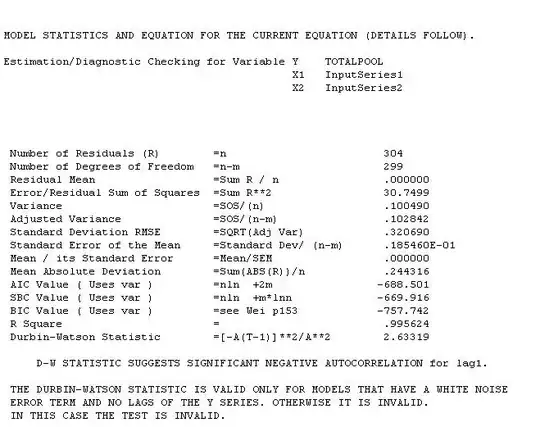enter image description here . The test for commonality is easily rejected with an F value of 79 with 3,291 df. Note that the DW statistic is 2.63 from the composite analysis. The summary of coefffici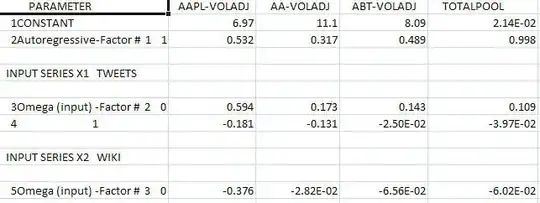enter image description hereents is presented here. The OP poster reflected that the only software he has access to is insufficient to be able to answer this thorny research question.

IrishStat
  • 27,906
  • 5
  • 29
  • 55
  • I have sent you my dataset yesterday. Have you had the time to take a look at it? Although I really appreciate your replies, they are beyond me. My knowledge end with performing a linear regression with a dataset that always has a Durbin-Watson around 2. That is all they have tought us at uni. Now, for my thesis, I have collected this data, unaware of the difficulties analyzing it. Your approach is too advanced for what my coach expects of me, so perhaps you could advice me on a less-advanced technique, available in SPSS? I will download AUTOBOX demo an have a look :-) – Pr0no Aug 08 '12 at 16:27
  • Please repost your data to this query as I have not received it and also send it to me at dave@autobox.com and I will try and help you. – IrishStat Aug 08 '12 at 20:03
  • MANY THANKS. Although I have a hard time understanding, I really appreciate your efforts. At least I now think it is safe to say there is no predictive value in the IVs. Since I'm limited to using SPSS (and only basic statistical knowledge), I would like to know whether it would be entirely wrong to use a OLS or ARIMA(1,0,0) to point out the same conclusions, if limitations of the model used are properly argumented. As suggested by @Charlie, I'm controlling somewhat for between company differences by adding a fixed effect dummy (see updated OP). Your thoughts, please. – Pr0no Aug 09 '12 at 14:30
  • 1
    I don't know what you meanthere is no predictive value inthe IV'S.There certainly is!From the 3 companiesI analyzed there appears to be statistically significantly different coefficients.It would be totally wrong to use OLS as there are outliers,there is a lagged relationship that you could use (contemporaneous,lag1 & lag2 for all 3 of your series) that could provide you with the coefficients of response BUT if you don't adjust for the anomalies this is futile.Adjusting for company differences by adding a dummy isadjusting the intercept/constant it does not adjust the regression coeffficients. – IrishStat Aug 09 '12 at 14:47
  • What I meant to say is that there are significant differences in the coefficients, and the coefficients are statistically significant, but as I understand no general conclusion can be drawn if the data isn't adjusted for anomalies (which I am unable to do in SPSS and with my knowledge). Therefore, I thought adding the dummy would be a viable alternative but as you point out it isn't. In the opening post, I performed 2 analysis myself: OLS with lagged DV as IV and autoregression with Prais-Winsten method. How does the latter relate to your analysis in terms of appropriateness? – Pr0no Aug 09 '12 at 15:10
  • 1
    Your model is inadequate as it doesn't (entirely !) capture the effect of the IV's . Not adjustng for anomalies defeats all that you are doing . You might want to see http://www.stat.sc.edu/~west/javahtml/Regression.html – IrishStat Aug 09 '12 at 15:25
  • I see and understand now. However, is there any - perhaps less sophisticated way - you know of to cleanse the dataset with SPSS? – Pr0no Aug 09 '12 at 16:02
  • You might run an OLS and then examine the residuals. Divide the residuals by the standard deviation from the ols model to obtain standardized residuals. Take the absolute value of these standardized residuals and select those points in time where the absolute value exceeds 3.0. For those time points replace the observed value with the original value minus the original residual for that point in time thus cleansing the observation. – IrishStat Aug 09 '12 at 16:35
  • Running OLS with same variables you used (using the dataset I send you) returns only 32 standardized residuals with an absolute value exceeding 3.0. I don't believe replacing those values that would do much. What is the basis for choosing 3 as the threshold? – Pr0no Aug 09 '12 at 16:55
  • Ok lag y twice ; lag tweets twice ; lag wik twice thus – IrishStat Aug 09 '12 at 17:32
  • the 3.0 is the 99.73% confidence t value. Use 2.5 instead and you will get more. Use an OLS model that includes the ouput series lagged once and twice ; include tweets contemporaneous and lag 1 and lag2 ; include wiki contemporaneous and lag1 and lag2 – IrishStat Aug 09 '12 at 17:40
  • still only 187 observations, does that suggest the number of anomalies is rather restricted? – Pr0no Aug 09 '12 at 18:58
  • 2
    Yes I would say that if you have 102 days and 86 companies , 187 anomalies might be a reasonable count. Just because this might be a small percentage DOES NOT MEAN that one shouldn't adjust. – IrishStat Aug 09 '12 at 19:31
  • Do I understand you correctly that if the 187 observations are adjusted, an OLS with contemporaneous, lag1 and lag2 dependent vars as independent in the regression provides an adequate model? If so, I understand an autoregression with Prais-Winsten (or Cochrane-Orcutt), without lagged variables, is equally explainatory, right? – Pr0no Aug 09 '12 at 20:34
  • 1
    No. I said to use the past of y and the past of y two periods AND tweets contemporary and lag1 and lag2 and wiki contemporary , lag1 and lag2 .THUS 8 INPUT SERIES and a constant . That would be sufficient. – IrishStat Aug 09 '12 at 21:04
  • Thanks again. I ran the regression on a subset (in reality, I also have Google SVI data, but for 12 companies there is no SVI data so I removed them from the set), see http://i.imgur.com/Ufiug.png. I want to thank you for your patience. If you have any more comments regarding this OLS, I would really like to hear them. What is surpising is that most predictive (apart form lags) seem to be TODAYS tweet volume but YESTERDAYS number of pageviews on Wikipedia. – Pr0no Aug 09 '12 at 21:34
3

There are a few things that I would do differently.

First, because each stock has a different overall level, you should include a set of ticker fixed effects, which is a set of dummy variables for whether a particular observation belongs to a particular ticker.

Second, stock prices are (almost?) always assumed to have a unit root. This would mean that the coefficient on your lagged variable would be 1. It is already pretty close (0.876); without fixed effects we can't be sure (because there could be bias), but it is pretty suggestive of a unit root.

For proper inference, you must look at the change in stock prices or the change in the log of the stock price (the latter is roughly equal to the % change or the return and is what is typically used). Otherwise you can get spurious results. As an added bonus, this differencing actually removes the need for ticker fixed effects.

Third, your standard errors are likely too small. You should employ standard errors that are clustered at the ticker level. This helps account for remaining serial correlation in the error terms.

These issues should be discussed in any reference to panel data, the usual moniker for data of the type that you are using. Wooldridge's Introductory Econometrics textbook for undergrads or Econometric Analysis of Cross Section and Panel Data for graduate students are common references.

Charlie
  • 13,124
  • 5
  • 38
  • 68
  • please notice that the dependent variable here is stock trading volume (total shares traded on that day), not stock prices. However, in reality stock returns (% of change between closing and opening price per day) and volatility (using PARK-method) are also dependent variables in my thesis. In the analysis above, the dependent variable is LN(stockVolume). I logged it because there's a lot of difference among companies concerning the number of traded shares. But if I understand you correctly, I should also take %change in stock volume, right? – Pr0no Aug 08 '12 at 16:11
  • 1
    Ahh, right, sorry. The 0.876 coefficient is high and worrisome, but it might be reduced when you add fixed effects. I don't know whether trading volume is typically thought of as a unit root process or not. There are unit root tests for panel data that you might employ, but try running the model with fixed effects and see what happens. – Charlie Aug 08 '12 at 18:00
  • I don't understand what you mean by "whether a particular observation belongs to a particular ticker". Could you please provide an example, for instance by editing the dataset in the opening post? The `200`, `150`, and `2423325` in line 1 all belong to company 1. This is evident from the dataset, right? What would a dummy add to that? – Pr0no Aug 08 '12 at 18:36
  • 1
    You would have 86 dummy variables. The first would be 1 if an observation is from company 1 and 0 otherwise. The second would be 1 if an observation is from company 2 and 0 otherwise and so on. – Charlie Aug 08 '12 at 21:30
  • I'm have never been confronted with econometrics before (I'm a business administration student and we've only had 1 statistics course going up untill OLS regression). Please see the updated opening post; I have added all dummies to my dataset. If I include them as independent variables in a simple OLS regression, am I then doing the right thing? – Pr0no Aug 09 '12 at 10:50
  • 1
    Unfortunately Wooldridge's books, albeit very good, are more suited for dealing with small $T$, large $N$ panel data problems. Here we have large $T$, so the usual assumption of homogeneity (i.e. all time series are follow the same model) is likely violated. The advice to use growths is spot on. Personally I would try to fit some model similar to ones Peter Pedroni analyses. Which basically means, doing individual regressions and looking at the distribution of coefficients, which is pretty much what @IrishStat is suggesting. – mpiktas Aug 09 '12 at 11:00
  • @Charlie - apart from the dummy variables for fixed effects (how should I include them in the analysis), I have added a control variable (marketRet: the return for the S&P100 that day - the researched companies are all S&P100 companies), at least I understood that marketReturn could be a control variable. But how do I add it to the analysis? I think I might stick with OLS or ARIMA(1,0,0) even though it is probably insufficient but after contacting my thesis coach, (since it's not econometrics I study), this is seen as sufficient. Your input, please. – Pr0no Aug 09 '12 at 14:25
  • Yes, add those variables to the righthand side of the OLS model. Also, you should try using differences of $y$, as I and mpiktas suggested. This should alleviate the time series problems. – Charlie Aug 13 '12 at 16:00
1

In some ways the models seem to agree quite a bit. The standard error of the estimates and the Durbin-Watson statistic are very similar between the two models. Also the constant term and the regressors hbVolLog and wikiLog are significant in both models. The main difference seems to be that the first model includes the lagged value of the dependent variable and that seems to account for the large increase in R square. So I see nothing strange about the results. it just points to the strength of the lagged variable in predicting StockVol0. What does puzzle me is why the adjusted R square is the same as the unadjusted rather than being somewhat lower.

Michael R. Chernick
  • 39,640
  • 28
  • 74
  • 143
  • Thanks for explaining the similarities between the models. I conclude from your reply that it is safe to assume the Durbin-Watson and standard error of the estimates. However, am I right to take from the models that I should report the second one if I want to exlain the predictive power of the independent vars on stockVol? If I report the first model, it is only predictive because of the lagged independend var, which is derived from the dependent var (so it is not suprising that it has a high beta, right?). – Pr0no Aug 08 '12 at 15:56
  • 1
    @Pr0no It seems that a model with good explanatory power requires the lagged variable. The second model shows the statistically significant but not strongly explanatory effect of the other covariates. – Michael R. Chernick Aug 08 '12 at 16:05
  • Right, so taken all together this means that tweet volume and the number of wikipedia pageviews have limited power in explaining stock trading volume, but yesterday's trading volume is very explainatory and tweets and pageviews marginally add to that explainatory power? – Pr0no Aug 08 '12 at 16:20
  • 1
    @Pr0no Yes that is what I would conclude from this. – Michael R. Chernick Aug 08 '12 at 16:31
  • I foresee that if I run AR(IMA) analysis, similar, but not exactly the same, could be concluded from that. Does that mean, in laymans terms, that there is no "one right answer" when analyzing data? I would have expected different models producing the same results but if I understand correctly, it is more a matter of argumenting why you choose a certain model and hence present those results, but acknowledge that with different arguments, another model with slightly different results could have been employed as well? – Pr0no Aug 08 '12 at 16:48
  • 1
    @Pr0no It is not the form of the model that matters here it is the inclusion or exclusion of variables in the model. The difference in results has to do with including or excluding the lagged variable only. – Michael R. Chernick Aug 08 '12 at 16:57
  • 2
    It is important to note that DW statistic reported most likely ignores the structure of data. I.e. it treats all data as long time series, instead of 86 different time series. So the usual OLS interpretation of DW statistic is not helpful here. – mpiktas Aug 09 '12 at 10:51
  • @mpiktas - how could I then account for the fact that there are 86 different timeseries, but still want to make general conclusions about the relationship between my independent and dependent vars? As you suggested, I could perform 86 separate OLS regressions, no problem, and if I understand you correctly the DW in each case would then have more meaning. If I follow you and IrishStat, I would store the coefficients of each regression and look at their distribution. But I'm lost from there on. What am I looking for in the distribution and what is the next step (as explained to a BA undergrad ;) – Pr0no Aug 09 '12 at 11:23
  • @Pr0no, there is no definite answer, but taking mean and standard deviation of resulting regression coefficients would be a good start. – mpiktas Aug 09 '12 at 12:25
-1

There are several possibilities in this problem, and really the best discussion I can cite is The Theory and Practice of Econometrics, 2nd edition, George Judege, W.E. Griffiths, R. Carter Hill, Helmut Lutkepohl, and Tsoung-Chao Lee, Wiley Series in Probability and Mathematical Statistics 1985, Chapter 13, Inference in Models That Combine Time Series and Cross-Sectional Data. Sounds dated, but I have been doing research with ridge regression that dips back into this resource. This was a big, very comprehensive book. Sorry I don't have more time to specifically analyse this, but I may do a post on this type of problem in my blog www.businessforecastblog.com

Clive Jones
  • 17
  • 1