Calculate Zipf-Mandelbrot parameters from distribution

Question

I am fetching trending topics from social media where the frequency of likes is said to follow a Zipf-Mandelbrot distribution; i.e., some of the posts will have a high number of likes and some other very few.

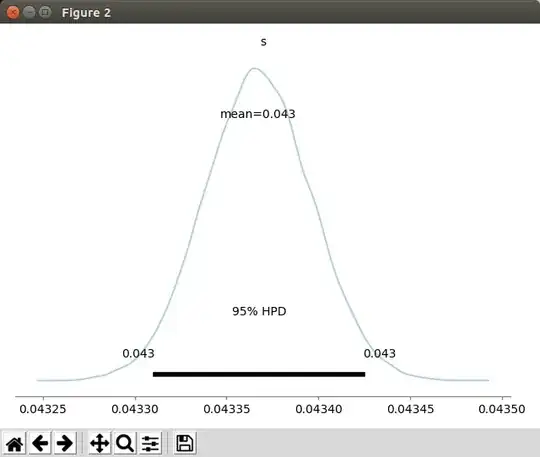
So far I collected about 100 thousand samples and I want to calculate the s and q parameters. I looked at the script described here. I ran the code on my data and it gives me the s parameter of s=0.043.

How do I calculate q?

The first figure is from the Python Powerlaw package.

PS: I'm a statistics newbie

The script in the answer generated the following warnings:

Warning messages:
1: In nlm(function(p) negloglik(p, x = x), p = c(20, 20)) :
  NA/Inf replaced by maximum positive value
2: In nlm(function(p) negloglik(p, x = x), p = c(20, 20)) :
  NA/Inf replaced by maximum positive value
3: In nlm(function(p) negloglik(p, x = x), p = c(20, 20)) :
  NA/Inf replaced by maximum positive value

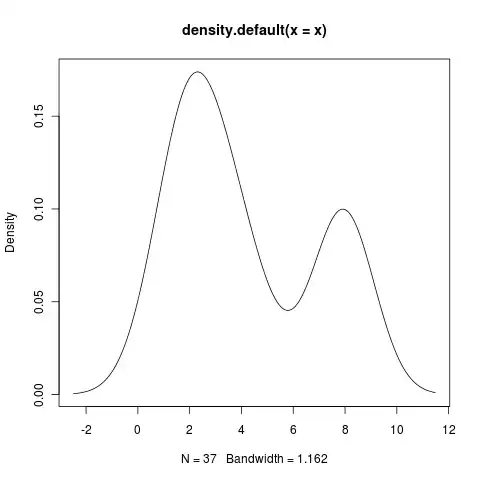
and this plot:

I modified the above script to fit my data:

> N <- 40480    # the size of my dataset
> x <- read.csv("dataset.txt")    # my dataset file
> negloglik <- function(parms, x=x) {
+     H <- sum(1/(1:N + parms[1])^parms[2])
+     -sum(log(1/(x + parms[1])^parms[2]/H))
+ }
> plot(d <- sapply(1:N, function(x) exp(-negloglik(c(5,5), x))))  # here I changed 10 to N (the size of my data)
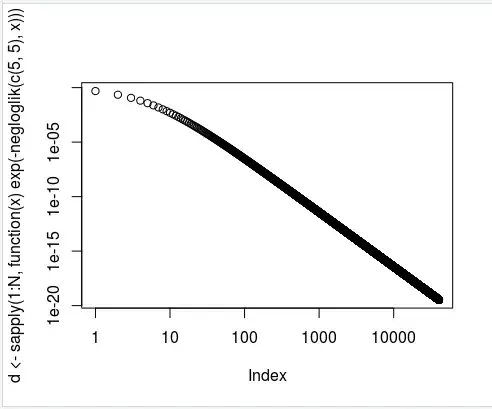
> x <- sample(1:N, 1000, replace = T, prob = d)
> ml <- nlm(function(p) negloglik(p, x=x), p=c(20,20))

This output the following graph: (xy log scale)

However, I got a similar warning message:

Warning message:
In nlm(function(p) negloglik(p, x = x), p = c(20, 20)) :
  NA/Inf replaced by maximum positive value

Just use maximum likelihood. I don't use Python, but there must be an optimizer, if not just build your own grid search. The density is a very simple one to implement. — AdamO, Apr 02 '18 at 15:47
@AdamO Do you use R? I'm trying to perform the MLE in R. The package PoweRlaw seems to do the job — Bruno Cortez, Apr 02 '18 at 19:56
As a semi-serious R programmer, I think learning how to fit general distributions is a great skill. I have an example here. — AdamO, Apr 02 '18 at 20:47

score 1 · Accepted Answer · answered Apr 02 '18 at 20:36

Maximum likelihood can be done. I'm a little surprised by how badly the ML estimates converge. Example R code is shown below for calculating the density and negative log likelihood based on the parametrization in the Wikipedia page:

$$f_x(x) = \left( \sum_{i=1}^N \frac{1}{(i + p)^s} \right)^{-1} \frac{1}{(x + p)^s}$$

set.seed(123)

## set a N = 10
N <- 10

## populate the negative log likelihood function
negloglik <- function(parms, x=x) {
  H <- sum(1/(1:N + parms[1])^parms[2])
  -sum(log(1/(x + parms[1])^parms[2]/H))
}

## generate pmf for sampling
plot(d <- sapply(1:10, function(x) exp(-negloglik(c(5,5), x))))

## draw a random sample with n=1000
x <- sample(1:10, 1000, replace = T, prob = d)

## calculate ml estimates
ml <- nlm(function(p) negloglik(p, x=x), p=c(20,20))

Calculate Zipf-Mandelbrot parameters from distribution

1 Answers1